Research on Multiobjective Optimization and the SEAMO Algorithms

Christine Mumford (Valenzuela)

1  Overview of Research

The main contribution of my work on multiobjective optimization is the algorithm SEAMO (a Simple Evolutionary Algorithm for Multiobjective Optimization) and the various improved versions, particulary SEAMO2. The main advantages of using SEAMO algorithms are as follows:
The only issue with SEAMO is that it can be poor compared to other MOEAs on problems where solutions are extremely unevenly spread across the Pareto front. For example they perform poorly on specially contrived benchmark problems designed to test the limitations of MOEAs.

2  Introduction to multiobjective optimization

Many real-world applications require the simultaneous optimization of several (often competing) objectives For example:
There are four main approaches to solving multiobjective optimization problems:
  1. Optimize for one of the objectives and model the other objectives as hard constraints.
  2. Weighted sum - combine all the objectives into a single scalar value, and optimize the scalar value.
  3. Solve for the objectives in a hierarchical fashion, optimizing for a first objective then, if there is more than one solution, optimize these solutions for a second objective, and repeat for a third etc. if appropriate.
  4. Obtain a set of alternative, non-dominated solutions, each of which must be considered equivalent in the absence of further information regarding the relative importance of each of the objectives.
The fourth method is used here, and this has the advantage that no a priori decisions have to be made regarding the relative importance of the different objectives. Using this approach a set of viable alternatives are presented to the decision maker, providing excellent options that may be missed using other methods.
Evolutionary algorithms are particularly effective for multiobjective optimization, because they work on a population of points, and so can generate sets of solutions that trade-off the different objectives. SEAMO is an example of a multiobjective evolutionary algorithm (MOEA). For an introduction to multiobjective optimization I recommend the book by Kalyanmoy Deb [8].
Key to an understanding of multiobjective optimization is the concept of Pareto dominance. Optimization using a single objective produces one optimum solution. Using a multiobjective method generates a set of non-dominating solutions, each of which is equally good in its own way. For example, consider one of the examples given above: that of minimizing the weight and maximizing the strength of an aircraft design. A set of solutions will consist of options of varying weights and strengths, for which the lighter designs will have less strength and the heavier designs will be stronger. Thus, there will be a tradeoff to consider, to find a design that is strong enough but not too heavy.
Pareto Dominance  
Solutions are vectors, f = (f1,f2,…fn), for any two solutions f1 and f2, f1 is said to dominate f2 if these conditions hold: If one of the above conditions does not hold f1 does not dominate f2.
What makes a good MOEA?  
An effective Pareto-based multiobjective EA will converge on a solution set with the following properties:
Example Problem – the multiple knapsack problem  
drag1.png
Single knapsack problem: Multiple knapsack problem:
Object
number		Knapsack 1,
Capacity = 38 		Knapsack 2,
Capacity = 35
WeightProfitWeightProfit
19233
28749
32421
47545
53693
66258
71742
83386
99731
103173
A possible solutions is:
   
{2, 3, 4, 5, 6, 7, 9}
   
Packing these objects into the 2 knapsacks - is the solution feasible? First check that capacity of neither knapsack is exceeded.
   
K1 {w1 = 36, p1 = 38}, K2 {w2 = 31, p2 = 29}, thus, neither capacity is violated, and the solution vector is {38, 29} ({profit in knapsack 1, profit in knapsack 2}.
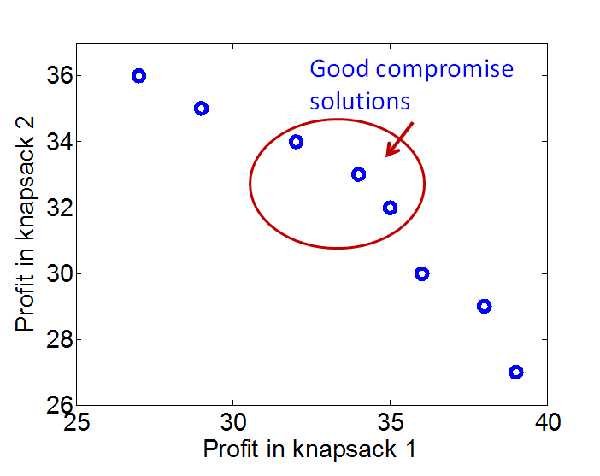
Profit K1Profit K2Objects selected
3927{2,3,4,5,7,8,9}
3829{2,3,4,5,6,7,9}
3630{2,3,5,6,7,8,9}
3532{2,3,4,6,7,8,9}
3433{2,3,4,5,6,8,9}
3234{2,4,6,7,8,9,10}
2935{1,2,3,4,5,6,8}
2736{1,2,4,6,7,8,10}
Good compromise solutions for a dual objective multiple knapsack problem
compromise.png

3  Main themes of my research

The main contribution has been the SEAMO algorithms, which are much quicker and easier to implement than other MOEAs. SEAMO algorithms have also produced competitive results.
Procedure SEAMO2
Parameters: N - population size, stopping condition
Begin
Generation of the initial set of solutions:
   Generate N random individuals
   Evaluate the objective vector for each individual
            and store it
   Record the bestSoFar for each objective function
Main loop
   Repeat
      For each member of the population
         This individual becomes the first parent
         Select a second parent at random
         Apply crossover to produce offspring
         Apply a single mutation to offspring
         Evaluate the objective vector
            produced by the offspring
         If offspring objective's vector
            improves on any bestSoFar
            Then it replaces a parent
         Else if offspring is a duplicate
            Then it dies
         Else if offspring dominates either parent
            Then it replaces it
         Else if offspring is neither dominated by
             nor dominates either parent
            Then it replaces another individual
             that it dominates at random
         Otherwise it dies
      End for
   Until stopping condition is satisfied
   Print all non-dominated solutions in the final population

4  Downloadable Documents

My work culminated in several research papers. [1] is the first paper that was written on SEAMO and introduces the algorithm. [2] describes some experiments to establish which representations and operators work best on the multiobjective 0/1 knapsack problem. [3] deals with some improvements to SEAMO (SEAMO2). [4] and [5] describe how further improvements can be obtained by splitting the population into a hierarchy of subpopulations, each working on a different part of the Pareto space. Although the algorithm is becoming more complicated in these papers, the results are quite impressive. Also, this approach provides some ideas and motivation for possible parallel implementation. [6] compares SEAMO2 with SPEA2 [9] and MOGLS [10] on benchmark multiple knapsack problems. Finally, [7] describes a more detailed study using the original SEAMO. The Chapter also gives a simple introduction to multiobjective optimization.
Quick overviews are available for some of the papers, where the conference presentations are included. I have my husband, Mark Mumford, to thank for drawing the dragon cartoons.
Note: SEAMO-style algorithms are used for examination timetabling and the urban transit routing problem.

Papers

       This Research

[1]
Valenzuela, Christine L, A Simple Evolutionary Algorithm for Multi-Objective Optimization (SEAMO), IEEE World Congress on Computational Intelligence (WCCI2002): Congress on Evolutionary Computation (CEC2002), 12 - 17 May 2002, Honolulu, Hawaii, pp. 717-722. DOI link.Conference presentation.
[2]
Mumford, Christine L, Comparing Representations and Recombination Operators for the Multi-Objective 0/1 Knapsack Problem, Congress on Evolutionary Computation (CEC2003), 8 - 12 December, Canberra, Australia, 2003, 854-861. DOI link.Conference presentation.
[3]
Mumford, Christine L., Simple Population Replacement Strategies for a Steady-State Multi-Objective Evolutionary Algorithm, Genetic and Evolutionary Computation Conference (GECCO), Seattle, Washington, USA 2004, 1389-1400. Publisher's link. Conference presentation.
[4]
Mumford, Christine L., A hierarchical approach to multi-objective optimization, IEEE Congress on Evolutionary Computation (CEC) Portland, Oregon USA 2004, 1944-1951. DOI link. Conference presentation.
[5]
Mumford, Christine L., A Hierarchical Solve-and-Merge Framework for Multi-Objective Optimization, IEEE Congress on Evolutionary Computation (CEC) Edinburgh, Scotland, 2005, 2241-2247. DOI link. Conference presentation.
[6]
Colombo, Gualtiero and Mumford, Christine L., Comparing Algorithms, Representations and Operators for the Multi-objective Knapsack Problem, IEEE Congress on Evolutionary Computation (CEC) Edinburgh, Scotland, 2005, 1268-1275. DOI link.
[7]
Mumford, Christine L. A Simple Approach to Evolutionary Multi-Objective Optimization. Chapter 4 in ‘Evolutionary Multiobjective Optimization: Theoretical Advances and Applications’, edited by Ajith Abraham, Lakhmi Jain and Robert Goldberg. Springer Verlag, London, 2005, 55-80. Publisher's link.

References

[8]
Deb, Kalyanmoy, Multi-Objective Optimization Using Evolutionary Algorithms, John Wiley & Sons, 2001.
[9]
Zitzler, Eckart; Laumanns, Marco; and Thiele, Lothar, SPEA2: Improving the Strength Pareto Evolutionary Algorithm, Computer Engineering and Networks Laboratory (TIK), Department of Electrical Engineering, Swiss Federal Institute of Technology (ETH) Zurich, TIK-Report 103, May 2001.
[10]
Jaszkiewicz, On the performance of multiple-objective genetic local search on the 0/1 knapsack problem - a comparative experiment, IEEE Transactions on Evolutionary Computation, Vol. 6 (4), 2002, pp 402 - 412.


File translated from TEX by TTH, version 3.87.
On 29 Dec 2010, 09:09.