1 Introduction

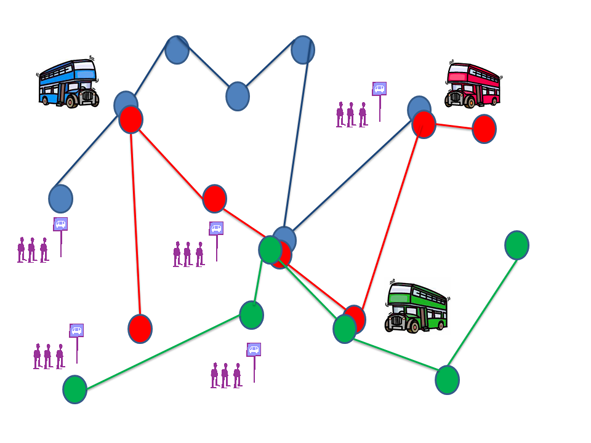
The urban transit routing problem (UTRP) involves devising routes for public transport systems: for example, buses or trains. It is a highly complex NP-Hard problem, and solving it invariably involves a cycle of generating and testing “candidate” route sets.

Unlike better known vehicle routing problems (such as the travelling salesman problem, or the capacitated vehicle routing problem) the UTRP is difficult to formulate mathematically. In many ways, there is much more freedom in constructing the routes. A particular node (e.g., bus stop or train station) or set of nodes can appear on many different routes, and individual routes can be long or short (or even circular). A route set can contain few or many routes. The design of the optimum route set will vary according to certain factors, including vehicle capacity (how many passengers it can carry), vehicle frequency (i.e., the schedule or timetable), and the demand between each pair of nodes (i.e, the numbers of passengers wishing to travel from node A to node B). In practice, the evaluation of automatically generated candidate route sets can prove both time consuming and challenging, with huge numbers of potential solutions rejected because they are infeasible, i.e., they fail to meet demand or perhaps they leave some passengers stranded without connections. Heuristic and metaheuristic methods are clearly appropriate for NP-Hard problems such as this, but the solution methods need to be very carefully designed, and incorporate a level of “intelligence” or knowledge about the problem, to control the amount of “randomness” involved, to avoid wasting time generating and testing huge numbers of infeasible solutions.

Once feasible route sets are generated, we then have the difficult issue of evaluation, which requires choosing an appropriate path through the travel network for each passenger, and using this information to calculate statistics, such the average travel time over all demand on the network, and the average number of transfers per person. There may be several different potential paths through the travel network of an individual passenger, and various decision have to be made, such as whether it is better to transfer vehicles and change routes if it saves time, or stay on an vehicle to avoid the inconvenience of making transfers. In our work so far we have adopted the relatively simple model published by Chakroborty et al ([1, 2] to determine the assignment of travel paths, using an all-pairs-shortest-path approach with 5 minutes penalty for each person-transfer that is made.

For further reading, two recent review articles are recommended, [3, 4]. The book written by Christoph Mandl (1979) [5]is well worth reading. It is a pioneering text which introduces many of the important ideas. Another good introductory read is a report from the University of Texas [6] published in 1994.

2 Main themes of the research

Despite the obvious importance of the UTRP, progress is hampered by a lack of text-book style models and benchmark problems. The only publicly available benchmark with all necessary information is Mandl’s 15 node Swiss Road Network Problem, which is very small indeed. Published work that goes beyond Mandl’s data tends to focus on bespoke systems for specific urban locations, where the necessary data is not provided for other researchers. Compared with other important NP-Hard problems (such as the travelling salesman problem, the examination timetable problem, the job-shop scheduling problem, and many more), the “focal point” for academic research seems to be weak for the UTRP, and it is difficult for researchers to compare their methods with one another.

2.1 The Work of Lang Fan and Christine Mumford, 2005 - 2009

In this work research Lang Fan and Christine Mumford built on the work of Mandl and Chakroborty et al and developed a basic heuristic/metaheuristic framework for iterative solution improvement. We recognized that all successful solution improvement methods rely on the following THREE fundamental aspects for their ultimate success:

1. the quality of the chosen representation,
2. the effectiveness of the initialization procedures, and
3. the suitability of the chosen neighbourhood moves.

Regardless of whether the method eventually chosen is tabu search, simulated annealing, evolutionary algorithms, variable neighbourhood search, or some other heuristic/metaheuristic method, these fundamental issues of representation, initialization and neighbourhood moves are key. We concentrated on building a successful framework incorporating a suitable representation and simple but effective initialization procedures and neighbourhood moves. Avoiding the time-consuming evaluation of vast numbers of weak or infeasible solutions, is probably the main challenge we encountered during our research. We tested our framework using simple hill-climbing and simulated annealing algorithms, and beat previously best published results for Mandl’s benchmark problem. In addition we generated some new test instances (which unfortunately are now lost) and established some simple upper and lower bounds for the UTRP.

Our work culminated in two research papers [7, 8] and, in 2009, a PhD was awarded to Lang Fan.

2.2 Further Work by Christine Mumford 2011 - 2013

A couple of year after the completion of Lang Fan’s PhD, Christine Mumford began to slowly advance the work, because of its fascination and obvious global importance. A great debt to Lang is owed, his work provided some sound foundations to upon which to move forward. Everything was newly coded from scratch using MATLAB, with a few C routines linked in for speedup (for example, Floyd Warshall all pairs shortest paths). New data sets were created, because unfortunately our previous data was either miss-labelled or lost. All code was thoroughly and carefully tested during development.

The new work involved the development of a multiobjective evolutionary algorithm with new heuristics, mutation and crossover operators. Results have recently been published in [9].

2.3 Designing Efficient Routes and Schedules for Public Transport Systems 2013 - 2014

This project was partially funded by HPC Wales and ran from the beginning of October 2013 to the end of September 2014. The team working on the project are listed below:

Christine Mumford (Principle Investigator)

Rhyd Lewis (Co-Investigator)

Ian Cooper (Research Associate)

Andrew Olden (Research Associate)

Matthew John (PhD Student associated with the project, funded by the School of Computer Science & Informatics)

The project focussed on:

• Implementing parallel models of multi-objective evolutionary algorithms on HPC resources
• Visualization of road networks and bus routes
• Generation of data sets

Two publications have resulted from this work, one directly covering the parallel models [10], and the other relates more to the PhD work of Matthew John, [11]. Recently a paper has been submitted by Matthew John, Christine Mumford, Rhyd Lewis and Jonathan O’Connell to IEEE Transactions on Evolutionary Computation covering Surrogate Models, GPU speedup and some detailed experiments to evaluate the contributions of various genetic operators to our multi-objective evolutionary algorithm for bus routing.

3 Current and Future Work

• Christine Mumford is working with Rhyd Lewis and Penny Holborn in collaboration with the Vale of Glamorgan Council on School bus routing.
• Christine Mumford is also working with Sergio Nesmachnow from the University of the Republic, Uruguay, on a short collaborative project funded by the British Embassy in Uruguay.
• New funding is being applied for.

Data

There are currently 15 data files.

These were files were contributed by Christine Mumford (C.L.Mumford@cs.cardiff.ac.uk) to whom questions should be directed

There are five data sets in fifteen files consisting of an (x, y) coordinates file, a transit demand matrix and a transit time matrix for each of the five urban transit routing problem:

1. Mandl’s Swiss Network (15 Nodes and 21 Links Network). Files MandlCoords.txt, MandlDemand.txt, and MandlTravelTimes.txt
2. Mumford0 (30 Nodes and 90 Links Network). Files are Mumford0Coords.txt, Mumford0Demand.txt and Mumford0TravelTimes.txt.
3. Mumford1 (70 Nodes and 210 Links Network). Files are Mumford1Coords.txt, Mumford1Demand.txt and Mumford1TravelTimes.txt.
4. Mumford2 (110 Nodes and 385 Links Network). Files are Mumford2Coords.txt, Mumford2Demand.txt and Mumford2TravelTimes.txt.
5. Mumford3 (127 Nodes and 425 Links Network). Files are Mumford3Coords.txt, Mumford3Demand.txt and Mumford3TravelTimes.txt.

The structure of the coordinates files are as follows:

The structure of the Demand and Travel Times files are 2D matirces:

Please note:

1. The transit time between each pair of nodes is measured by minutes.
2. The transit time is recorded as ”Inf” between nodes that are not directly connected.
3. All the matrices are symmetric.
4. The row and column headings (i.e., node numbers) are not included in the matrix.

Mandl’s Swiss Network was published in his book: (C.E.Mandl,Applied Network Optimization,Academic,London,1979)

Experimental results for the networks have been published in my paper [9]

Click here to access to download a zip file with this data plus an explanatory document and some timing experiments.

Click here to use an online evaluation tool for evaluating your own route sets, according to the constraints we use in our papers defined in Table 1. All our results assume a 5 minute waiting time / transfer penalty. Please note that there is a runtime limit of 30 seconds on the website, so this program will only work on relatively small instances. For example, it will work on route sets for Mandl, Mumford0 and Mumford1, but probably time out for route sets derived from larger networks (e.g., Mumford2 and Mumford3). (A Python program for download is in preparation and will be posted soon). The evaluation software gives researchers the opportunity to ensure that their results are comparable with ours. Over a period of time we have found that errors in the evaluations procedure can be very tricky to detect, and we believe that we have now ironed them all out. This has been achieved by different researchers independently coding the evaluation procedure, followed by cooperation to debug and validate.

Click here to download Mandl test files to try out the program (TravelTimes, Demand and a 6 route solution).

References