Research on Graph Colouring and the University Examination Timetabling Problem

Christine Mumford (Valenzuela)

1 Introduction

A simple version of the university examination timetabling problem maps exactly into a graph colouring problem.

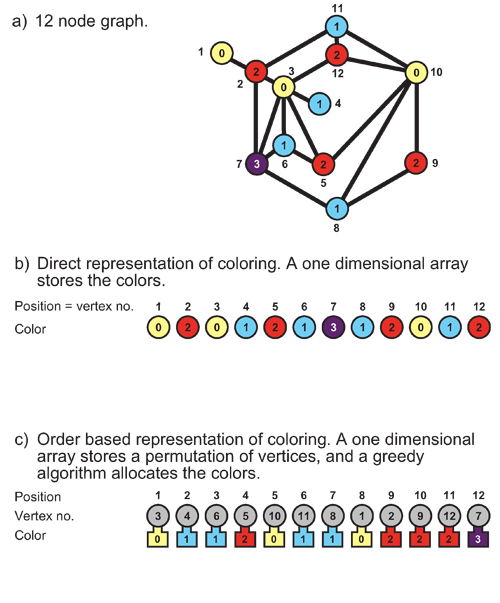
Graph Colouring Given a graph consisting of a set of vertices and connecting edges, colour the nodes with a minimum number of colours, such that no adjacent nodes have the same colour. Part a) of the figure below illustrates a 12 node graph, showing a possible colouring. Note that all adjacent nodes have different colours. Four different colours are used here. The question arises whether it is possible to colour this graph using less than four colours, without violating the adjacency constraint. In Part a) of the figure, the numbers outside the nodes correspond to node numbers, and the numbers inside the nodes denote colour codes (i.e., yellow = 0, blue = 1, Red = 2, and Purple = 3).

Examination Timetabling A simple examination timetabling problem involves scheduling examinations in consecutive equal-length timeslots, in such a way that no student is timetabled to take more than one exam at a time. The objective is to minimize the total length of the timetable.

In the exam timetabling problem:

Colours correspond to time slots,
Nodes correspond to exams, and
An edge between a pair of nodes indicates that there are students taking both exams, so the exams cannot be scheduled in the same time slot.

Encoding / Representation This is an important issue. Given an optimization problem to solve, we need to find a way of encoding potential solutions. There can be many very different encodings for the same problem, and each different representation can produce a very different shape to the solution search space.

Part b) in the figure above shows a simple direct encoding for the graph colouring/timetabling problem, in which we have a one-dimensional array, with the indices representing node ID numbers (or exams) and the array contents holding the assigned colour (or timeslot). For example, node 1 is allocated the colour yellow (0) and node 2 the colour red (1).

Part c) in the figure illustrated a permutation representation in which the one dimensional array holds a permutation of node IDs (exams). This is an example of a method known as an indirect encoding, and the permutation relies on a greedy decoder to assign the colours (or timeslots). A greedy decoder will work down the list, starting at position 1 of the array, and assign to each node (exam) the lowest integer (or earliest) colour (timeslot) that is feasible, without violating and problem constraints. In our example, the first node on the permutation list is node 3, and this is allocated yellow (0). The second node on the list is allocated red (1), because it is adjacent to node 3, and therefore cannot be assigned the same colour as node 3. It is the role of a good ordering (or reordering) heuristic to present the greedy decoder with a suitable permutation that it can transform into a high quality solution (more on this later).

More on University Examination Timetabling Avoiding timetable clashes is an example of a hard constraint, which must always be obeyed. In reality, it is common to have additional hard constraints, such as:

There is probably limited space - only a maximum number of seats available
The exams will probably have to fit into a certain number of weeks, so that it does not overlap with classes or the vacation
Certain exams (such as laboratory tests) may require specific resources which are only available in certain rooms
Some exams may be restricted to days/times when part-time students are attending

Hard constraints must be adhered to. soft constraints, on the other hand, represent desirable criteria for timetabling, but are more flexible and do not have to be obeyed. Examples of soft constraints include:

Minimize the timetable length (e.g., the number of slots)
Maximize the spread of exams for individual students - to give plenty of time between exams for final revision
Schedule exams with large numbers of students earlier, to give plenty of time for marking

Sometimes it may be impossible to solve a problem that obeys all of the hard constrains: for example, the minimum timetable length may exceed the maximum number of weeks available - what happens then? Hard constraints may be reformulated as soft constraints, if schedule difficult to come up with (e.g., minimize the number of clashes).

2 Main themes of my research

The main contribution of my work has focussed on using permutation-based representations. Although most authors favour a direct approach to encoding, rather than using a permutation and decoder, for me order based techniques have one powerful advantage: every permutation decodes as a feasible solution, on the other hand, direct approaches do not guarantee legal solutions.

As mentioned above, the trick is to present the greedy decoder with a permutation sequence that it can process into a high quality solution. Much of my work involves evolutionary algorithms working on a permutation representations. To pre-process the permutations I make extensive use of the iterative grouping and reordering heuristics of Culberson and Luo [5]. These heuristics, applied to the graph colouring and simple timetabling problems, possess a very interesting property:

it is impossible to get a worse coloring by rearranging the color classes in the ways described by Culberson and Luo, and it is possible that a better coloring (using fewer colors) may result.

3 Downloadable Documents

My work culminated in several research papers, four of which are downloadable as offprints below. The first paper is on graph colouring, the next two on examination timetabling and the final one is on the minimum span frequency assignment problem, a problem which is closely related to graph colouring and timetabling.

The main contribution of [1] is to introduce two new and effective order-based crossover/local search combinations:

Permutation One Point (POP), and,
Merge Independent Sets (MIS).

The effectiveness of the new operators is demonstrated in two ways:

by showing that much better results can be achieved with the crossovers than without them,
by comparing their performance on DIMACS benchmarks with other order based crossovers.

[2] explores a simple bi-objective evolutionary approach to the examination timetabling problem. The new algorithm handles two hard constraints: 1) avoiding examination clashes and 2) respecting the given maximum seating capacity; while simultaneously minimizing two objective functions: 1) the overall length of the examination period and 2) the total proximity cost. The bi-objective evolutionary algorithm attempts to pack all the examinations into as short a period as possible while, at the same time, favoring a good spread of examinations for individual students.

[3] extends the work began in [2] to introduce a new greedy algorithm that simultaneously optimizes proximity costs (to attempt to ensure an even spread of examinations for individual students) as well as timetable length, and incorporates sophisticated local search methods.

The genetic algorithm (GA) described in [4] breeds permutations of transmitters for minimum span frequency assignment, and uses a greedy decoder in a similar way to the above graph colouring and examination timetabling problems. The approach hybridizes employs a dynamic re-ordering technique called Generalized Saturation Degree to seed the initial population, and several permutation operators from the GA literature are compared. This work predated and inspired my work on graph colouring and examination timetabling. There are some proofs with respect to the effectiveness of Culberson's and Luo's reordering heuristics on the minimum span frequency assignment problem.

Papers

[1]: Mumford, Christine L. New Order-Based Crossovers for the Graph Coloring Problem. Parallel Problem Solving from Nature IX (PPSN IX), Reykjavik, Iceland, 2006, LNCC 4193, 880-889, Springer, 2006. DOI link.
[2]: Mumford, Christine L. An Order Based Evolutionary Approach to Dual Objective Examination Timetabling. Proceedings of the 2007 IEEE Symposium on Computational Intelligence in Scheduling (CI-Sched 2007), Honolulu, Hawaii, 2007. DOI link.
[3]: Mumford, Christine L. A multiobjective framework for heavily constrained examination timetabling problems. Annals of Operations Research, Vol 180 (1) 2010 pp 3 - 31. (Also first published on line in 2008). DOI link.
[4]: Valenzuela, Christine L. A Study of Permutation Operators for Minimum Span Frequency Assignment using an Order Based Representation. Journal of Heuristics Vol. 7(1) pp 5-21, Kluwer Press 2001. DOI link.

References
[5]: J. Culberson and F. Luo, Exploring the k-colorable landscape with iterated greedy, In Johnson and Trick [6], pages 499-520.
[6]: D. S. Johnson and M. A. Trick, Editors, Volume 26 of DIMACS Series in Discrete Mathematics and Theoretical Computer Science, American Mathematical Society, 1996.

File translated from T_EX by T_TH, version 3.87.
On 29 Dec 2010, 06:55.