


Next: Relaxation Labelling Methods
Up: Model Based Object Recognition
Previous: Tree Search Methods
Basically many constraints have been developed in order to produce efficient
search heuristics. Here we describe some popular methods which illustrate a
broad range of heuristics.
The Oshima and Shirai Method (1979)
This method was one of the first methods
developed to deal with a variety of classes of objects and to be able to recognise a
scene described by depth maps containing multiple objects in any orientation.
Objects are considered to have planar surfaces, smoothly curved
surfaces or both. The classes of smoothly curved surfaces
allowed include ellipsoids, hyperboloids,
cones, paraboloids and cylinders.
This method operates in two stages.
- The Learning Phase
-
This method does not use any stored solid model representation to perform matching.
Instead models are constructed from images of the objects to be recognised.
Thus, a learning phase takes place in which known objects are individually
shown to the system in different poses. A description of each object is
built up, in terms of properties of surfaces and their relationships, to
create a model of the object.
The description is made using the segmentation of curved and planar
surfaces from individual images. The segmentation method employed by Oshima and
Shirai is a basic region growing method except that many surface properties and
interrelationships are also calculated. These then are represented in a
relational graph or semantic network. Typical surface properties
for each region include:
- surface type (plane, cylinder etc.),
- number of adjacent surfaces,
- area,
- perimeter,
- minimum, maximum and mean radii from the surface centroid to the boundary,and
- the standard deviation of the radii from the surface centroid to the
boundary.
The relationships between surfaces are characterised by:
- distance between surface centroids,
- angle between best fit planes to this and neighbouring regions (if the
surface is curved the best fit plane is still used for this measure),
- type of
intersection -- classed as convex, concave, mixed (if intersection is not concave
or convex) or no intersection.
Only a discrete set of views are used to model an object. Thus, for a complete
model description of an object to be compiled, all unique views of the object
must be presented to the system.
- The Matching Phase
-
This phase operates by trying to match the set of visible regions observed in a
scene to each object view in a database of learned object descriptions.
Not all surfaces present in the corresponding model view of the scene may be
present in the observed scene description because of occlusion or poor segmentation,
so a procedure that restricts incorrect matchings is required. This is
achieved by initially driving the search with observed data and then, when
a suitable set of scene features have been successfully matched with the model,
model data is used to efficiently guide the rest of the search (see
Fig. 56
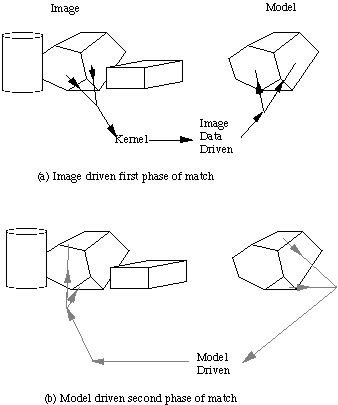
Fig.  Oshima and Shirai matching method
The image data driven part of the search involves constructing one or more
kernels , each of which contains one or two regions that provide the
best potential matches to an object model. The chosen regions are selected according
to the criteria that they should, if possible, be planar, have large area, and have
many neighbours. The criteria are relaxed until ideally two regions or
at worst one region for the kernel is found.
Oshima and Shirai matching method
The image data driven part of the search involves constructing one or more
kernels , each of which contains one or two regions that provide the
best potential matches to an object model. The chosen regions are selected according
to the criteria that they should, if possible, be planar, have large area, and have
many neighbours. The criteria are relaxed until ideally two regions or
at worst one region for the kernel is found.
The model database is then searched for matches starting with the best kernel. If
no match is found then another kernel is selected. If only one match is found
using this kernel then the model driven matching phase is invoked. If more than
one match is found then other possible kernels are also considered. The system
suspends any further matching for kernels which give more than one match until all
other kernels providing a single match have been considered by the model driven
phase. Note that at the end of the matching process there could be more than one
interpretation for a given kernel.
The model driven matching process of the second phase involves searching the scene
around the kernel for regions corresponding to those in the model. The search is
controlled by a similar type of depth first tree search that which we have
already described.
At all stages regions are considered to be matched if a similarity function
, based on region properties and relationships, is below a certain
threshold.
When a match for a particular kernel has been found, a candidate body
is said to have been found in the scene. The matching process continues until
all scene regions have been tested for participating in a match. If only one
candidate body is found in the scene then it is accepted as the desired match.
Otherwise the scene requires further interpretation. If there are multiple
candidates, they are examined to filter out inconsistent interpretations: two
candidate bodies must be inconsistent if they share a region. For each kernel found
a candidate body is rejected if one or more of its features are included in another
candidate body which is consistent with respect to the same kernel. At the end of
this process, hopefully one or perhaps more sets of mutually consistent
interpretations will remain. Each such combination gives a possible interpretation
of the scene from which position and orientation information can be calculated.
The 3DPO Method (1983)
The 3DPO (Three-dimensional Part Orientation) vision
system was developed by Bolles and his colleagues
to recognise and locate parts from depth maps for the purposes of directing a robot
arm to grasp a wide range of moderately complex industrial parts. To achieve
this goal they argued that most current vision strategies did not provide the
required generality, being based upon simple generic object types such as
polyhedra, cylinders, spheres or surface patches. Instead they adopted an entirely
different approach that could recognise objects using only a few features or
feature clusters that highly constrain the object (such as a circle
with a fixed radius) and consequently the size of the solution search space.
These ideas are now known as local feature focus methods.
The matching process consists of five stages:
- Primitive Feature Detection
- -- Here low-level
features are segmented and
linked together. Edges are detected in the three-dimensional data. Edges are
classified as being convex, concave
or step edges.
- Feature Cluster Formation
- -- The aim of this
stage is to form clusters of (primitive) features that can be used to hypothesise
the type, position and orientation of the object. Thus coplanar edge clusters
are formed and circular arcs are separated out, for example.
- Hypothesis Generation
- -- A search is made of the database of models to
find a match. The strategy used here is to test individual clusters first and if
these are not sufficient then groups of clusters are tested. It is at this stage
that the feature focus approach is used by searching for object specific clusters
such as circles of a certain radius.
- Hypothesis Verification
- -- Next,
any hypotheses formed are tested by looking for additional features in the image
that are consistent with each given hypothesis.
- Parameter Refinement
- --
In this final stage a given verified hypothesis is interrogated again in order
to produce a more accurate location for the part. Averaging or least squares
techniques are applied during this step.
This matching process uses an extended solid
model. Here a form of boundary model) is
augmented with a feature classification network. The feature network classifies features according to type and size, and
groups features that share common surface normals, common axes (for cylinders)
etc.
The ACRONYM Method (1979)
Brooks has developed a vision system,
ACRONYM, that recognises three-dimensional objects occurring in two
dimensional images. The examples given in the papers involve recognising airplanes
on the runways of an airport from aerial photographs. He uses a generalised cylinder
approach
to represent both stored model and objects extracted from the image. . As in Nevatia and
Binford's method (See next section), a relational graph
structure is used to store the representation.
Nodes are the generalised cylinders and the links represent the relative
transformations (rotations and translations) between pairs of cylinders.
The system also uses two other graph structures, which are constructed from the
object models, to help in the matching strategy:
- Restriction Graph
- -- This graph represents
constraints on classes of objects, in order to make generic part
descriptions more specific. An example given by Brooks considers classes
of electric motors. These can be described by a generic motor type which is
then divided into more specific classes of motors such as motor with a base, motor
with flanges. These can then be further described in terms of functional classes
(dependent on use) such as central heating water pump or gas pump.
Additional constraints are allowed to be added to the graph during the recognition
process.
- Prediction Graph
- --
Links in this graph represents relationships between features in the image.
The links are labelled must-be, should-be or exclusive according to
how likely it is that a given pair of features will occur together in a single
object.
Since the image is only two-dimensional account must be taken of the
projection of the three-dimensional object features into two
dimensions. Brooks uses two descriptions for two-dimensional features:
- Ribbons
- -- These are
used to describe a projection of a body made of generalised cylinders. Note
that Nevatia and Binford use a three-dimensional
form of ribbon.
- Ellipses
- -- These are used to describe the projection
of the ends of a generalised cylinder. For ends of a circular cylinder the
projections are exactly ellipses. For polygonal cross-sections, ellipses
can provide a description of the ends by fitting the best circle or ellipse through
the vertices and noting the projection of this shape.
The matching process is performed in two stages:
- The image is searched for local matches to ribbons derived from the stored
model. Such instances of ribbon matches are grouped into clusters.
- The clusters are checked for global consistency in that each match must
satisfy both the constraints of the prediction graph, and the accumulated
constraints of the restriction graph.
This work has been extended by Kuan and Drazowich to permit use of
three-dimensional images. The basic principles of ACRONYM are adhered to but
surface properties are incorporated. Also, numerical feature measurements are used
during matching (whereas there is a purely symbolic use of features in the original
method). The surface properties are included in a multilevel representation of
objects which is used in the prediction phase. The levels and the features
represented at each level are:
- Object Level
- -- stores, for example, spatial relationships between
object components, object dimensions, view point characteristics such as minimum
and maximum size, and occlusion relationships between features.
- Generalised cylinder level
- -- stores cylinder contour, cylinder position
and orientation, cylinder dimensions, relationship between edges etc. This
level is very important since generalised cylinders are the basic representation of
objects in the system. Specific cylinder properties are therefore kept separate
from more general surface characteristics.
- Surface Level
- -- describes surface type, edge boundary
information, and spatial surface relationship.,
- Edge Level
- -- records edge types
(step, convex, concave etc.).
The Grimson and Lozano-Perez Method (1984)
This method was originally designed to match sparse oriented surface
points (points on an object with a surface normal attached)
but has also been extended to match straight edges by
Murray (1988) and others. Here we discuss the method
in terms of matching straight line edges in a scene to straight line edges of a
model, based on the work by Murray, as edges are more suitable than points when
dense depth data is available. However, the discussion is equally valid for the
case of oriented surface points. The only differences are that the points are
matched to planar model faces and the implementation of some geometric
constraints is slightly different.
The method requires the following assumptions:
- The image data have been segmented to provide edges that are accurate to
within some specified error. This error is specified in terms of the positioning of
the end points and an uncertainty cone for the direction of the edge. Oriented
surface point errors are specified in terms of a small volume of error.
- The objects to be recognised can be modelled as polyhedra.
This method is divided into two stages:
- An exhaustive set of feasible interpretations of the sensed data is produced. Interpretations consist of
pairings of each sensed edge with some stored model edge. Interpretations
inconsistent with local edge constraints derived from the model are simply discarded. The edge constraints are
said to be local since they are derived from knowledge of neighbouring edges only
and not from overall knowledge gained from the whole view or object model.
- Each feasible interpretation is tested for consistency with the
object model. An interpretation is allowable if it is possible to provide
a rotation and translation that places each sensed edge in correspondence
with a model edge to within some specified error.
The two stages are now described separately.
Generating Feasible Interpretations
If an object model contains m edges and there are s sensed edges in the
scene then there are 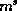 possible sets of complete interpretations which
match each sensed edge with some model edge. Only a few interpretations lead to
satisfactory solutions. Even for simple three-dimensional objects the number of
possible interpretations is very large. For example, a view of a cube can show up
to nine out of a possible twelve edges giving
possible sets of complete interpretations which
match each sensed edge with some model edge. Only a few interpretations lead to
satisfactory solutions. Even for simple three-dimensional objects the number of
possible interpretations is very large. For example, a view of a cube can show up
to nine out of a possible twelve edges giving 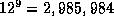 possible
interpretations of which 24 are plausible. It should be noted that this number
can be very much larger greater still when sampled oriented points are employed
instead of edges. Clearly it is not possible to exhaustively test all these
interpretations for a match so the basic idea is to exploit some simple, local
geometric constraints on the sensed edges to minimise the number of interpretations
that must be tested explicitly.
possible
interpretations of which 24 are plausible. It should be noted that this number
can be very much larger greater still when sampled oriented points are employed
instead of edges. Clearly it is not possible to exhaustively test all these
interpretations for a match so the basic idea is to exploit some simple, local
geometric constraints on the sensed edges to minimise the number of interpretations
that must be tested explicitly.
The possible pairings of sensed and model edges are represented in the form
of a search tree, called an interpretation
tree.
At each level of the tree, one of the edges from the scene is matched with each
of the m possible edges in the model. Each node has m children representing
taking the match proposed so far together with all possible matches for the current
scene
edge. The result is a tree where complete paths to the deepest level
correspond to complete matchings of object and scene edges. In the example shown
in Fig. 55, we assume (unrealistically) for the purposes of
illustration that the model has 4 edges and 3 edges have been found in the scene.
Thus the pairings ((1,2),(2,1),(3,1)) corresponds to edge 1 in the scene
matching edge 2 in the model, edge 2 in the scene matching edge 1 in the
model and edge 3 in the scene matching edge 1 in the model. Note that because
of errors in segmentation and other causes such as partial
occlusion, it may be possible for more than one edge in the scene
to correctly match a single edge in the model.
The interpretation tree is searched in depth first manner and pruned by
rejecting interpretations that fail to meet one or more local geometric
constraints. If the test is unsuccessful the current node and all
of its descendants may be rejected as none of
these descendants can possibly correct the current mismatch. In this way the
potentially large search space is controlled.
The three local geometric constraints employed to prune the interpretation
tree are:
- Distance Constraint
- -- The length of the sensed edge must be less than
or equal to the length of the model edge under consideration.
- Angle Constraint
- -- The angle between two adjacent sensed edges must
agree with that between the two corresponding matched model edges.
- Direction Constraint
- -- Let
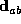 represent the range of
vectors from any point on sensed edge a to any point on sensed edge b. In an
interpretation which respectively pairs sensed edges a and b with model edges
i and j, this range of vectors must be compatible with the range of vectors
produced by i and j.
represent the range of
vectors from any point on sensed edge a to any point on sensed edge b. In an
interpretation which respectively pairs sensed edges a and b with model edges
i and j, this range of vectors must be compatible with the range of vectors
produced by i and j.
The constraints used if matching oriented surface points to planar model faces are
simpler:
- Distance Constraint
- -- The distance between each pair
of sensed points must be a possible distance between the corresponding faces.
- Angle Constraint
- -- The angle between each pair of
oriented sensed points must be compatible with that between the known surface
normals of the corresponding faces.
- Direction Constraint
- -- The vector linking two sensed points must lie
in a direction which lies within the range of all possible vectors going between
the respective surfaces they belong to.
An advantage of this constraint based approach is that all the model information
required by the constraints can be computed off-line and stored in look up
tables. Any information that is required for comparisons is then simply
referred to as needed.
Model Testing
This second stage involves interrogating the sets of possible interpretations which
are left after the first stage in order to firstly, estimate the transformation
(rotation, scale and translation) between scene and model coordinates, and
secondly, to check that all edges or surface points under the estimated
transformation lie within acceptable bounds of the assigned edges or assigned
faces.
The transformation is estimated by fitting the scene's description to
the matched model edges. Two approaches can be applied to solve the
problem. The first approach involves simply averaging the estimates of the
transformation obtained for each matching pair. Details
of the mathematics involved in this approach can be found in Grimson and
Lozano-Perez's original paper or the Marshall and Martin Book. Alternatively, to
produce more stable results, an approach similar to the estimation of
rotation and translation presented in Marshall and Martin Book may be employed.
This method is due to Faugeras and Hebert and has been
employed by Murray and in the TINA
vision system (discussed shortly).
Related Grimson and Lozano-Perez Methods
Apart from the Murray matching algorithm, several other approaches have been
developed over recent years based on the Grimson and Lozano-Perez method.
In particular Sheffield University's AI Vision Research Unit (AIVRU) have extended
this strategy for their TINA vision
system. This will be described in the next Section.
Lozano-Perez and Grimson have also developed their strategy to take into account
overlapping and mismatching faces. This is achieved by
incorporating an extra branch at each node in the interpretation tree to allow
for null matches. This technique is described in detail later in
Marshall and Martin Book as well as their papers..
Ikeuchi has developed a method for object manipulation tasks. He
generates an interpretation tree from object views and then proceeds to orientate
and locate objects in the scene
using extended Gaussian images.
Recently, Brady and his colleagues have proposed a method of recognising objects
described by parameterised models. They aim to
allow recognition of objects that do not have or do not require explicit or fixed
representations. The example cited in the paper is that of a vision system mounted
on an autonomous guided vehicle navigating around a factory environment. This
system must recognise wooden pallets used for stacking. A pallet can have many
valid forms which humans readily recognise. However, a system using
fixed object models would only be able to recognise an observed pallet if it
were lucky enough to have a model of that particular pallet. To overcome this a
parameterised object model is used where each wooden slat's position 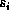 relative to some reference point is allowed to vary in the
model, as shown in Fig. 57. The value of each
parameter
relative to some reference point is allowed to vary in the
model, as shown in Fig. 57. The value of each
parameter 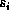 is determined in the matching process along with the rotation and
orientation.
is determined in the matching process along with the rotation and
orientation.
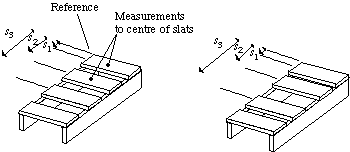
Fig.  Parameterised representation of a pallet
The TINA Method
Parameterised representation of a pallet
The TINA Method
Sheffield University's AI Vision Research Unit (AIVRU) have developed
a matching strategy for their TINA
vision system. Much of their work has recently been published
as a book containing a collection of papers related to the TINA vision
system and other important aspects of three-dimensional model-based
matching. Their method uses an approach similar to that
of Grimson and Lozano-Perez except that the depth-first tree
search is replaced by a hypothesise and test strategy. This
grows feasible interpretations in order to improve the efficiency of the
search. When some information in a scene may be missing (for example, when
occlusion of an object occurs) tree searches tend to be
combinatorially explosive. The hypothesise
and test strategy is driven by selecting features from the image based on feature
sizes and neighbourhoods. This
hypothesise and test strategy is similar to the feature focus} methods used in the 3DPO matching algorithm
discussed in for 3DPO.
The system matches three-dimensional edges (obtained by the use of passive
stereo) to three-dimensional edge based models.
The matching algorithm uses similar pairwise local geometric relationships to those
of Grimson and Lozano-Perez and Murray to limit
the search space further.
The basic method is as follows:
- A edge is chosen from the model to focus the search on. The
edge is determined on the basis of its length and the relative length of other
edges within a predefined distance from it.
- A set of edges close to
the focus edge that exceed some predefined length is determined.
- Potential matches to the focus edge are identified
in the image on the basis of their length.
- This set of potential matches is narrowed down by testing for consistency
with neighbouring edges.
- This set of matches is searched for
maximally consistent subsets that can be represented by a single matching
transformation (rotation and translation). The subsets must contain at least a
certain minimum number of elements. Subsets that represent the same transformation
are merged.
- Each subset is extended by adding new matches for all edges in
the scene which are consistent with the current set of matches.
- The extended subsets are ranked on the basis of number and length of
their elements.
- A final transformation is recovered using the least squares method of
Faugeras and Hebert mentioned above.
The Faugeras and Hebert Method (1983)
This method matches primitive surfaces extracted from a scene to ones in
the model. In the original approach the method is described
as coping with planar and quadric surfaces.
The basic approach is to try to match each primitive surface from the model, say
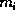 , to one segmented from the scene,
, to one segmented from the scene, 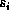 , to obtain a match pair
, to obtain a match pair 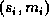 . This is achieved using a tree search similar to the interpretation tree described
earlier. However, an estimation of the transformation (rotation and translation)
describing the mapping from model to scene is used as a constraint to control the
search as it proceeds, in contrast to the previous methods based on the Grimson and
Lozano-Perez method where the transformation is
only estimated after matching is completed.
. This is achieved using a tree search similar to the interpretation tree described
earlier. However, an estimation of the transformation (rotation and translation)
describing the mapping from model to scene is used as a constraint to control the
search as it proceeds, in contrast to the previous methods based on the Grimson and
Lozano-Perez method where the transformation is
only estimated after matching is completed.
From a small initial set of match pairs, the match list, an
initial estimate of the transformation is made. Pairs of primitives from the
scene and model are then added to this list if they are compatible with the match
so far. Each time a successful match is found a new estimate of the transformation
is calculated, and the process is continued until all scene primitives have been
matched. If at any stage no possible match pair can be found then a backtracking
mechanism is used. A match is considered to be successful if it is consistent with
the existing transformation within
an allowed tolerance.
Thus, the method exploits the global constraint of rigidity
under the transformation to control the
potentially combinatorially explosive search space. This is a major difference from
the Grimson and Lozano-Perez method. The resulting paradigm of the Faugeras
and Hebert method is that of recognising whilst locating, which is controlled mainly
by global geometric constraints and not by testing a set of locally generated
feasible interpretations. The use of global
geometric constraints to control the search is generally
more efficient.
At each step the estimation of the transformation is found by solving a
least squares minimisation problem (not considered here -- details Marshall
and Martin Book or original papers).
A cheap constraint is also employed at each level of the search in
order to eliminate grossly mismatching pairs more quickly. The purpose of these
tests is to provide a rough estimate of the geometric consistency of the new pair
with the current match list. This test can be either or both of:
- The angle between a matched primitive in the scene and the current scene
primitive is equal to the angle between the corresponding primitives in the model to
within a given tolerance. Any previously matched scene primitive can be used in
principle to implement the constraint although usually one of the first matched
primitives is employed since we can order scene primitives before the matching
process to make the matching process more efficient. This can be done by choosing
the best segmented features or the features most likely to define the matching
transformation completely early on in the search or both.
- The angle between the current scene primitive and the current model
primitive rotated by the current estimation of the rotation is equal to
zero, to within a given tolerance.
This method has been used in many different computer vision applications. It has
been employed in matching in the two-dimensional domain, matching
different depth maps and matching using simple
occluding (or jump) edges and surface
primitives. In the last case Hebert and Kanade argue that
because segmentation of high order surface patches is unreliable, low level
primitives should be used first to obtain a small number of possible solutions
which are then tested using a detailed surface matcher. They employ simple
occluding edges which are easily and reliably calculated to limit the number of
possible interpretations.



Next: Relaxation Labelling Methods
Up: Model Based Object Recognition
Previous: Tree Search Methods
dave@cs.cf.ac.uk

![]() Oshima and Shirai matching method
The image data driven part of the search involves constructing one or more
kernels , each of which contains one or two regions that provide the
best potential matches to an object model. The chosen regions are selected according
to the criteria that they should, if possible, be planar, have large area, and have
many neighbours. The criteria are relaxed until ideally two regions or
at worst one region for the kernel is found.
Oshima and Shirai matching method
The image data driven part of the search involves constructing one or more
kernels , each of which contains one or two regions that provide the
best potential matches to an object model. The chosen regions are selected according
to the criteria that they should, if possible, be planar, have large area, and have
many neighbours. The criteria are relaxed until ideally two regions or
at worst one region for the kernel is found.
