

Next: Edge Linking
Up: Detecting Edge Points
Previous: Gradient based methods
All of the previous edge detectors have approximated the first order
derivatives of pixel values in an image.
It is also possible to use
second order derivatives to detect edges.
A very popular second order operator is the
Laplacian operator.
The Laplacian of a function f(x,y), denoted by
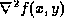 , is defined by:
, is defined by:
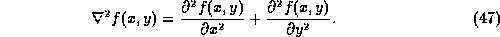
Once more we can use discrete difference approximations to
estimate the derivatives and represent the Laplacian operator
with the 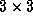 convolution mask
shown in Fig 25.
convolution mask
shown in Fig 25.
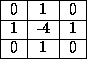
Fig. 25 Laplacian operator convolution mask
However there are disadvantages to the use of second order
derivatives.
- (We should
note that first derivative operators exaggerate the effects of
noise.) Second derivatives will exaggerated noise twice as much.
- No directional information about the edge is given.
The problems that the presence of noise causes when using edge detectors
means we should try to reduce the noise in an
image prior to or in conjunction with the edge detection process.
We have already discussed some methods of reducing or smoothing noise
in the Image Processing Section.
Some of these methods may be of use
here.
Another smoothing method is Gaussian smoothing
- Gaussian smoothing is performed by
convolving an image with a Gaussian operator which is defined
below.
- By using Gaussian smoothing
in conjunction with the Laplacian operator, or another Gaussian
operator, it is possible to detect edges.
Lets look at the
Gaussian smoothing process first.
The Gaussian distribution
function in two variables, g(x,y), is illustrated in
Fig. 26 and is defined by
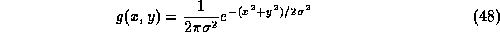
where  is the standard deviation representing the width of
the Gaussian distribution.
is the standard deviation representing the width of
the Gaussian distribution.
- The shape of the distribution and
hence the amount of smoothing can be controlled by varying
 .
.
- In order to smooth an image f(x,y), we convolve it with
g(x,y) to produce a smoothed image s(x,y) i.e. s(x,y) =
f(x,y)*g(x,y).

Fig. 26 The Gaussian distribution in two variables
Having smoothed the image with a Gaussian operator we can now take
the Laplacian of the smoothed image:
- Therefore the total operation
of edge detection after smoothing on the original image is
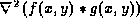 .
.
- It is simple to show that
this operation can be reduced to convolving the original image
f(x,y) with a ``Laplacian of a Gaussian'' (LOG) operator
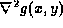 , which is shown in Fig. 27.
, which is shown in Fig. 27.
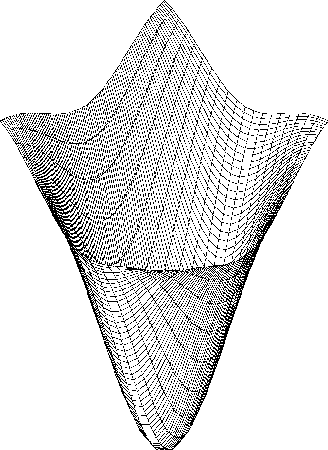
Fig. 27 The LOG operator
Thus the edge pixels in an image are
determined by a single convolution operation.
This method of edge detection was first proposed by Marr and
Hildreth at MIT who introduced the principle of the
zero-crossing method.
The basic
principle of this method is to find the position in an image where
the second derivatives become zero. These positions correspond to
edge positions as shown in Fig. 28.
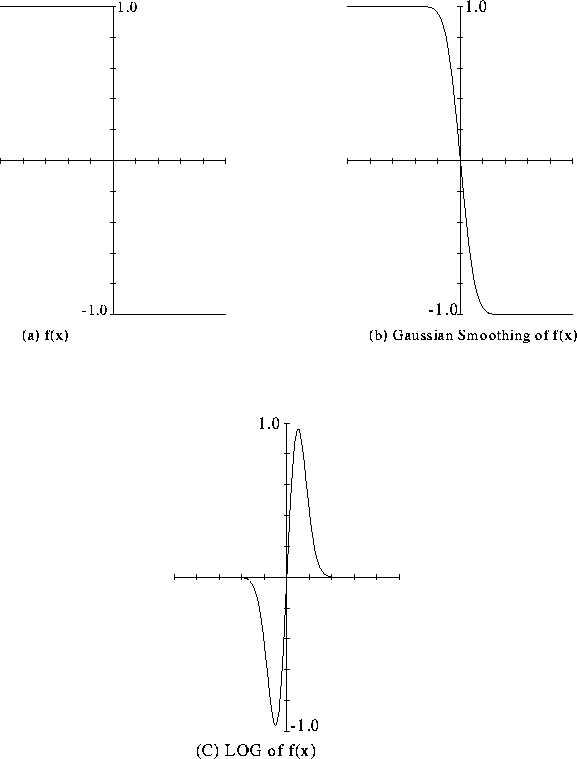
Fig. 28 Steps of the LOG operator
- The Gaussian function firstly smooths or blurs any step edges.
- The second derivative of the blurred image is taken; it has a
zero-crossing at the edge.
- NOTE: Blurring is advantageous here:
- Laplacian would be infinity at (unsmoothed) step edge.
- Edge position still preserved.
NOTE also:
- LOG operator is still susceptible to noise, but the effects
of noise can be reduced by ignoring zero-crossings produced by small
changes in image intensity.
- LOG operator gives
edge direction information as well as edge points - determined from the
direction of the zero-crossing.
A related method of edge detection is that of applying the
Difference of Gaussian (DOG) operator to an
image.
- computed by applying two Gaussian operators with
different values of
 to an image and forming the difference
of the resulting two smoothed images.
to an image and forming the difference
of the resulting two smoothed images.
- It can be shown that the DOG operator
approximates the LOG operator
- Evidence exists that the
human visual system uses a similar
method.
Another important recent edge detection method is the Canny edge
detector.
Canny's approach is based on optimising
the trade-off between two performance criteria:
- Good edge detection -- there should be low probabilities of
failing to mark real edge points and marking false edge points.
- Good edge localisation -- the positions of edge points marked
by the edge detector should be as close as possible to the real
edge.
The optimisation can be formulated by maximising
a function that is expressed in terms of
- The signal-to-noise
ratio of the image,
- The localisation of the edges
- A probability
that the edge detector only produces a single
response to each actual edge in an image.


Next: Edge Linking
Up: Detecting Edge Points
Previous: Gradient based methods
 David Marshall 1994-1997
David Marshall 1994-1997
![]() , is defined by:
, is defined by:
![]()
![]() convolution mask
shown in Fig 25.
convolution mask
shown in Fig 25.

![]()
![]() is the standard deviation representing the width of
the Gaussian distribution.
is the standard deviation representing the width of
the Gaussian distribution.