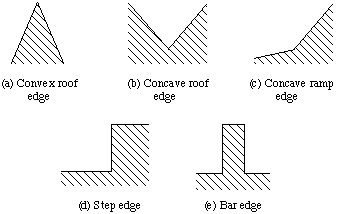
An edge point can be regarded as a point in an image where a discontinuity (in gradient) occurs across some line. A discontinuity may be classified as one of three types (see Fig 21):
Fig. 21 The C Compilation Model
Ramp edges have the same signs in the gradient components on either side of the discontinuity, while roof edges have opposite signs in the gradient components.
For example, if the pixel values are depth values,
If the pixel values are intensities,
The gradient is a vector, whose components measure how rapidly pixel values are changing with distance in the x and y directions.
Thus, the components of the gradient may
be found using the following approximation:
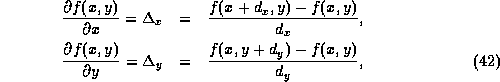
where ![]() and
and ![]() measure distance along the x and y
directions respectively.
measure distance along the x and y
directions respectively.
In (discrete) images we can consider ![]() and
and
![]() in terms of numbers of pixels between two points. Thus, when
in terms of numbers of pixels between two points. Thus, when
![]() (pixel spacing) and we are at the point whose
pixel coordinates are (i,j) we have
(pixel spacing) and we are at the point whose
pixel coordinates are (i,j) we have
![]()
In order to detect the presence of a gradient discontinuity we must
calculate the change in gradient at (i,j). We can do this
by finding the following gradient magnitude measure,
![]()
and the gradient direction,
![]() , given by
, given by ![]()
Implementation:
The difference operators in Eqn. 44 correspond to convolving the image with the two masks in Fig. 22.
This is easy to compute:
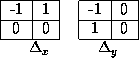
Fig. 22 Edge operator convolution masks
Instead of finding approximate gradient
components along the x and y directions we can also approximate
gradient components along directions at ![]() and
and
![]() to the axes respectively. In this case the
following equations are used:
to the axes respectively. In this case the
following equations are used:
![]()
This form of operator is known as the Roberts edge operator
and was one of the first
operators used to detect edges in images.
The corresponding convolution masks are given by:
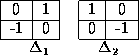
Fig. 23 The C Compilation Model
Many edge
detectors have been designed using convolution mask techniques,
often using ![]() mask sizes or even larger.
mask sizes or even larger.
An advantage of using a larger mask size is that errors due to the effects of noise are reduced by local averaging within the neighbourhood of the mask.
An advantage of using a mask of odd size is that the operators are centred and can therefore provide an estimate that is biased towards a centre pixel (i,j).
One
important edge operator of this type is the Sobel edge
operator. The Sobel edge operator masks
are given in Fig 24.
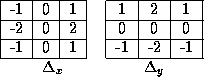
Fig. 24 Sobel edge operator convolution masks