As we know, the inside of a computer consists of many integrated circuits, where many transistors determine how the computer operates. And most of these integrated circuits are designed based on logic gates, i.e., AND gate, OR gate, NOT gate etc. A circuit made up of these logic gates relies on the level of the circuit to record data, we can be thought of as a desk lamp that records a "0", i.e., a high level, when it is on and a "1", i.e., a low level, when it is off, which is why computers systems are made up of binary "0" and "1". Let us back to the desk lamp problem, if there are only two states on the lamp-on and off, how can it count to 3?
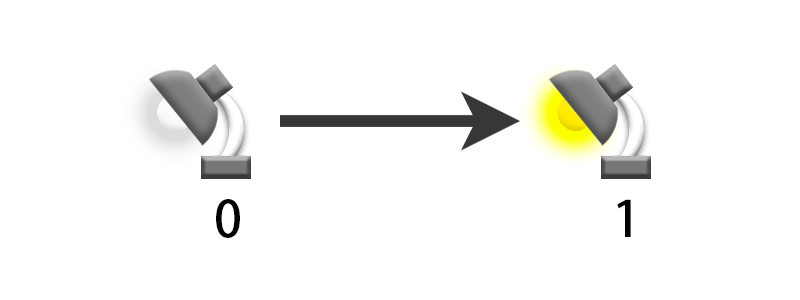
It is so easy! Think about how we count decimal numbers, when we count to 9, just moving forward becomes 10. Similarly, when counting to 2, add another lamp to represent that we got a 2. So that we could add more and more lamps to represent we got a “4”, an”8” and more!
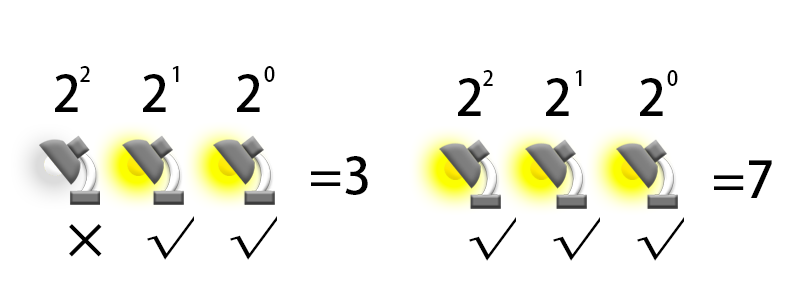
Now we have a “counter” which is made up of many lamps, also, do not forget the logic gates, Scientists have used a number of logic gates to create a special type of unit circuit, the latch, which holds signals in temporary storage to maintain a certain level state and is used to store data. Now the “counter” becomes a box because we can count the number and save it in the latch.
Now a new question arises, how do we change the data stored in the registers? We already know that we can represent larger data by adding some binary bits, and this makes it possible to show that in a computer, the computer can perform binary addition by shifting forward. So how does a computer perform subtraction internally? Let's imagine that we have a clock with the hour hand pointing to 10 o'clock, and we want to adjust this clock to 7 o'clock, how should we turn the hour hand? I think there are two ways to achieve this, the first is to rotate counterclockwise for 3 hours and the second is to rotate clockwise for 9 hours. Let's consider clockwise rotation as addition and counterclockwise rotation as subtraction.
In clockwise rotation we get an equation "10+9=19", in counterclockwise rotation we get another equation "10-3=7". In the first equation, the result is divided by twelve, and the remainder is 7, which means that the result is 7 after the modulo operation. In other words, a negative number will be exactly equivalent to a positive number under certain modulo conditions (e.g., -3(mod12) ≡ 9(mod 12)), and the two numbers are complementary to each other, so if the complement of a negative number can be found under (mod m), it can be equivalently replaced by the addition of a positive number by subtraction, and this complement is also known as the complement in computers. Now, we have a “counter”,” data box” and “operators, which means we got a minicomputer!
“Computational thinking is taking an approach to solving problems, designing systems and understanding human behaviors “(Wing, 2006).
Computational thinking is a methodology used to solve problems, and it is not only applied to solve problems within computers, but also to solve problems in life. Using computational thinking to solve problems can be roughly divided into the following steps:
Decomposing->Abstraction->Pattern recognition->Algorithms
In other words, analyze the problem, list the objects involved in the problem, the relationship between the objects, and the logical relationship between the steps in the process of processing the problem, to complete the preliminary design of the problem solution.
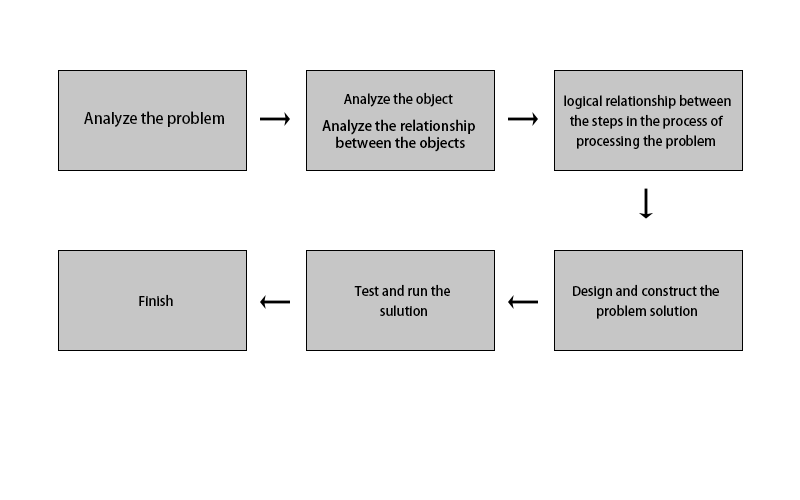
This is the first step in computational thinking, and the purpose of this step is to ensure the accuracy of the solution.
The next step is to eliminate redundant processes to achieve efficient problem-solving while ensuring that the solution is accurate.
1. To work accurately
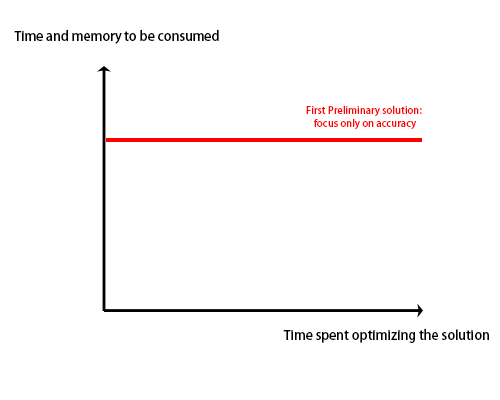
Let computational thinking be a methodology for solving practical problems in life. Computational thinking is the reformulation of a seemingly difficult problem into a problem that we know how to solve by analyzing, designing, and testing a solution to the problem, in which step we focus only on whether the problem is solved, providing a maximum value for our solution in terms of time and space consumption(The red line in the figure above indicates the resource consumption of the solution given the accuracy).
2. To make the work more efficient based on the accuracy
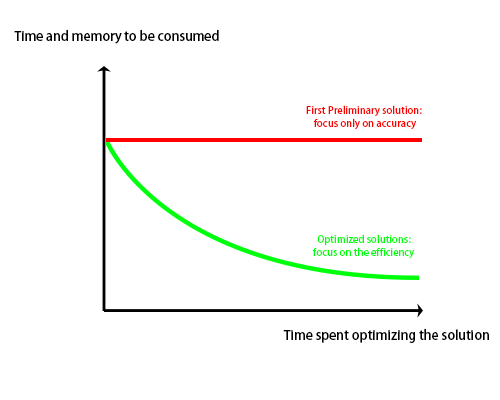
While ensuring the accuracy of the solution, we must also consider the machine's instruction set, resource constraints and operating environment(Wing, 2006), which is another important point of computational thinking, for example, how to make the physical space of the stored data more "close to each other" in the computer's memory structure so as to save memory space, and how to optimize The optimization of the algorithm to save running time should not result in the following situations:
1. Consume more time as well as space (memory) than the initial solution
2. The accuracy of the solution should not be missing in order to save time and space (memory)
Not only in the use of programming languages, but also in solving real-life problems, computational thinking should become a methodology for solving problems, which exists everywhere, in work and in life.
The following cartoon is a good representation of the way computational thinking approaches problems:

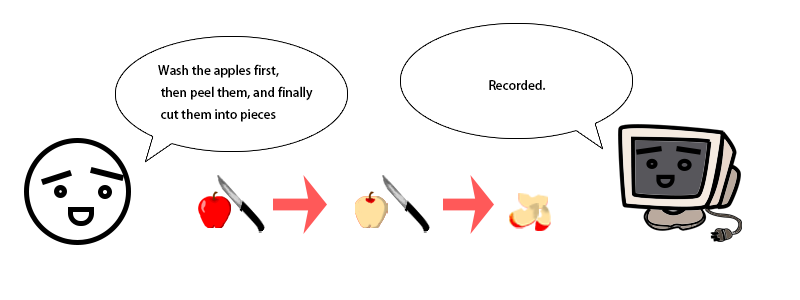
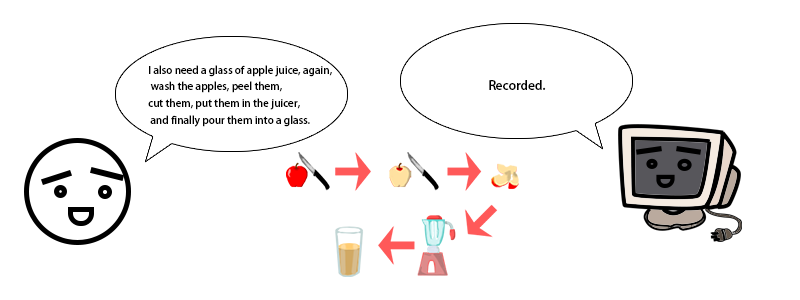

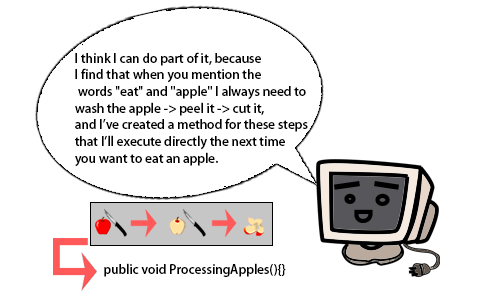



Brain-computer interface is a new technology that has been proposed in recent years, a technology for neuroscience, signal detection, signal processing, in addition, a highly relevant technology for neuronal signals, "fMRI", which analyses the occipitotemporal visual cortex by monitoring the blood oxygen level dependence (BOLD), thus enabling the simulation of images in people's minds(Nishimoto et al. 2011). Humans are moving closer to computational thinking, and it is in the direction of trying to understand human high-level language that computers are moving closer to human thinking.
In my future career planning and study, computational thinking is a skill that I should have and use skillfully, as mentioned above, not only should I consider the application of computational thinking when working with computers, but I should also use computational thinking in solving problems in daily life, just like using mathematical logic to solve problems. The application of computational thinking in relation to computing careers is most evident in the design of programs and algorithms, the previously mentioned "accuracy" and "efficiency".
The application of computational thinking in relation to computing careers is most evident in the design of programs and algorithms, the previously mentioned 'accuracy' and 'efficiency'. "Accuracy is the basic prerequisite for a programmer to be able to solve a problem, and efficiency is about retaining an edge over the competition in the same profession, the more efficient the programmer, the better the programmer.