Extended Gaussian Images

• Surface normal vector information for any object can be mapped onto a unit sphere, called the Gaussian sphere.
  
• Mapping is called the Gaussian image of the object.
  
• The mapping is: Surface normals for each point of the object are placed so that their
  
  
  • tails lie at the centre of the Gaussian sphere
    
  • heads lie on a point on the sphere appropriate to the particular surface orientation.

We can extend this process so that

• a weight is assigned to each point on the Gaussian sphere equal to the area of the surface having the given normal
  
• This mapping is called the extended Gaussian image (EGI).
  
• Weights are represented by vectors parallel to the surface normals, with length equal to the weight.

An example of such an extended Gaussian image is shown in Fig. 44.  

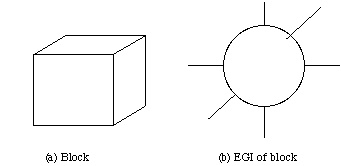
Fig. 44 The EGI of a block

Using three-dimensional solid models of objects (see next section),

• The corresponding EGIs for each stored object model can be computed and saved in the model database
  
• Model stored as a surface normal vector histogram.
  
• Surface normals easily extracted from Image (plane fitting)
  
• Once a match is found (by comparing EGI histograms) both the identity and orientation of the object may be calculated.

Disadvantages:

• EGIs only uniquely define convex objects.
  
• An infinite number of non-convex objects can possess the same EGI.

 

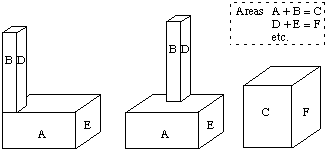
Fig. 45 Examples of objects with the same EGI