Region Splitting

The basic idea of region splitting is to break the image into a set of disjoint regions which are coherent within themselves:

• Initially take the image as a whole to be the area of interest.
  
• Look at the area of interest and decide if all pixels contained in the region satisfy some similarity constraint.
  
• If TRUE then the area of interest corresponds to a region in the image.
  
• If FALSE split the area of interest (usually into four equal sub-areas) and consider each of the sub-areas as the area of interest in turn.

• This process continues until no further splitting occurs. In the worst case this happens when the areas are just one pixel in size.
  
• This is a divide and conquer or top down method.

If only a splitting schedule is used then the final segmentation would probably contain many neighbouring regions that have identical or similar properties.

Thus, a merging process is used after each split which compares adjacent regions and merges them if necessary. Algorithms of this nature are called split and merge algorithms.

To illustrate the basic principle of these methods let us consider an imaginary image.

• Let denote the whole image shown in Fig 35(a).
  
• Not all the pixels in are similar so the region is split as in Fig 35(b).
  
• Assume that all pixels within regions 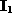, 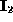and 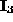respectively are similar but those in 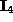are not.
  
• Therefore 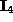is split next as in Fig 35(c).
  
• Now assume that all pixels within each region are similar with respect to that region, and that after comparing the split regions, regions 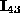and 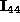are found to be identical.
  
• These are thus merged together as in Fig 35(d).

 

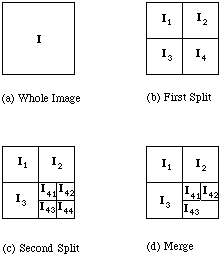
Fig. 35 Example of region splitting and merging

We can describe the splitting of the image using a tree structure, using a modified quadtree. Each non-terminal node in the tree has at most four descendants, although it may have less due to merging. See Fig. 36.

 

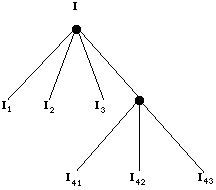
Fig. 36 Region splitting and merging tree