Fourier Space Smoothing Methods

Noise in an image means there are many rapid transitions (over a short distance) in intensity from high to low and back again or vice versa, as faulty pixels are encountered.

Therefore noise will contribute heavily to the high frequency components of the image when it is considered in Fourier space.

Thus if we reduce the high frequency components, we should reduce the amount of noise in the image.

We thus create a new version of the image in Fourier space by computing

where F(u,v) is the Fourier transform of the original image, H(u,v) is a filter function, designed to reduce high frequencies, and G(u,v) is the Fourier transform of the improved image.

Ideal Low Pass Filter

The simplest sort of filter to use is an ideal lowpass filter, which in one dimension appears as shown in Fig. 16.

 

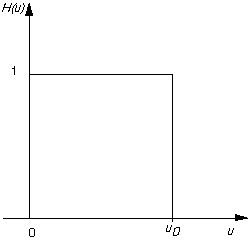
Fig. 16 Lowpass filter

This is a top hat function which is 1 for u between 0 and , the cut-off frequency, and zero elsewhere.

So All frequency space space information above is thrown away, and all information below is kept.

The two dimensional analogue of this is the function

where is now the cut-off frequency.

Thus, all frequencies inside a radius are kept, and all others discarded.

The problem with this filter is that as well as the noise, edges (places of rapid transition from light to dark) also significantly contribute to the high frequency components.

Thus an ideal lowpass filter will tend to blur edges become blurred.

The lower the cut-off frequency is made, the more pronounced this effect becomes.

Low Pass Butterworth Filter

Another filter sometimes used is the Butterworth lowpass filter. In this case, H(u,v) takes the form

where n is called the order of the filter. This keeps some of the high frequency information, as illustrated by the second order one dimensional Butterworth filter shown in Fig. 17, and consequently reduces the blurring.

 

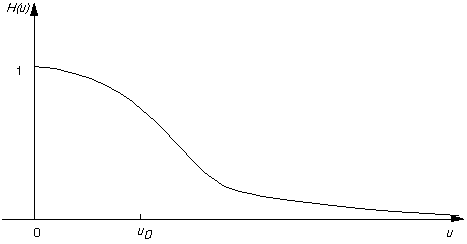
Fig. 17 A Butterworth filter