
Next: Fourier Transforms and Convolutions
Up: Fourier Methods
Previous: Fourier Theory
Several important optical
effects can be described in terms of convolutions.
Let us examine the concepts using 1D continuous functions.
The convolution of two functions f(x) and g(x), written f(x)*g(x), is defined
by the integral
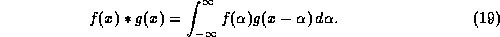
For example, let us take two top hat functions of the type
described earlier. Let 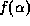 be the top hat function shown in
Fig. 11,
be the top hat function shown in
Fig. 11,

and let 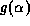 be as shown in Fig. 13,
defined by
be as shown in Fig. 13,
defined by

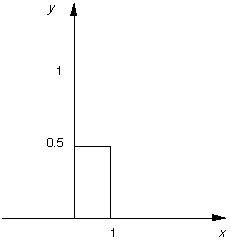
Fig. 13 Another top hat: 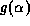
-
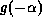 is the reflection of this function in the vertical
axis,
is the reflection of this function in the vertical
axis,
-
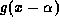 is the latter shifted to the right by a distance x.
is the latter shifted to the right by a distance x.
- Thus for a given value of x,
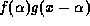 integrated over all
integrated over all
 is the area of overlap of these two top hats, as
is the area of overlap of these two top hats, as 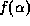 has unit
height.
has unit
height.
- An example is shown for x in the range
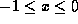 in
Fig. 14.
in
Fig. 14.
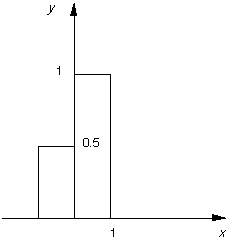
Fig. 14 Convolving two top hats
If we now consider x moving from 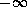 to
to 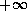 , we can see
that
, we can see
that
- for
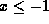 or
or 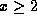 , there is no overlap;
, there is no overlap;
- as x goes from -1 to 0 the area
of overlap steadily increases from 0 to 1/2;
- as x increases from 0 to 1,
the overlap area remains at 1/2;
- and finally as x increases from 1 to 2, the
overlap area steadily decreases again from 1/2 to 0.
- Thus the convolution of
f(x) and g(x), f(x)*g(x), in this case has the form shown in
Fig. 15,
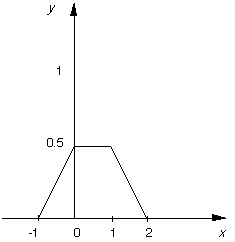
Fig. 15 Convolution of two top hats
Mathematically the convolution is expressed by:
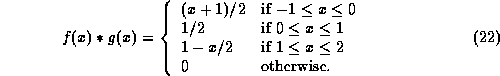
 David Marshall 1994-1997
David Marshall 1994-1997
![]()
![]() be the top hat function shown in
Fig. 11,
be the top hat function shown in
Fig. 11,
![]()
![]() be as shown in Fig. 13,
defined by
be as shown in Fig. 13,
defined by
![]()
![]()
![]() to
to ![]() , we can see
that
, we can see
that