Introduction to Stereo Imaging -- Theory

Let us consider a simplified approach to the mathematics of the problem in order to aid understanding of the tasks involved.

We will consider a set up using two cameras in stereo. -- other methods that involve stereo are similar.

Let's consider a simplified optical set up:

 

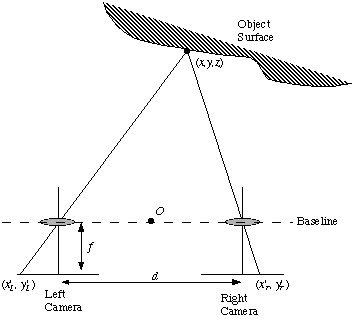
Fig. 5 A simplified stereo imaging system

Fig. 5 shows:

• 2 cameras with their optical axes parallel and separated by a distance d.
  
• The line connecting the camera lens centres is called the baseline.
  
• Let baseline be perpendicular to the line of sight of the cameras.
  
• Let the x axis of the three-dimensional world coordinate system be parallel to the baseline
  
• let the origin O of this system be mid-way between the lens centres.

Consider a point (x,y,z), in three-dimensional world coordinates, on an object.

Let this point have image coordinates and in the left and right image planes of the respective cameras.

Let f be the focal length of both cameras, the perpendicular distance between the lens centre and the image plane. Then by similar triangles:

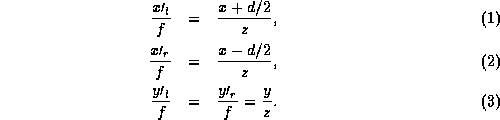
Solving for (x,y,z) gives:

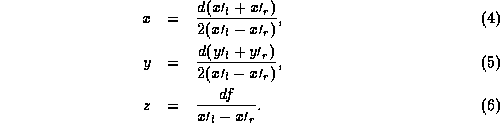
The quantity which appears in each of the above equations is called the disparity.

There are several practical problems with this set up:

• Near objects accurately acurately but impossible for far away objects. Normally, d and f are fixed. However, distance is inversely proportional to disparity. Disparity can only be measured in pixel differences.
  
• Disparity is proportional to the camera separation d. This implies that if we have a fixed error in determining the disparity then the accuracy of depth determination will increase with d.

However as the camera separation becomes large difficulties arise in correlating the two camera images.

In order to measure the depth of a point it must be visible to both cameras and we must also be able to identify this point in both images.

As the camera separation increases so do the differences in the scene as recorded by each camera.

Thus it becomes increasingly difficult to match corresponding points in the images.

This problem is known as the stereo correspondence problem.