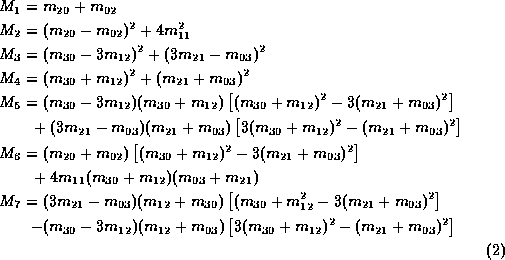Invariants

We can use simple descriptions (one numeric value) to represent features on and hence recognise objects:

• They provide a simple means of comparison.
• They can provide position and orientation information (i.e. Moments etc.)
• Too simplistic for some applications
• Do not give a unique means of identification.

Such numeric or statistical descriptions may be divided into two distinct classes:

• Geometric descriptions: area, length, perimeter, elongation, compactness, moments of inertia.
• Topological descriptions: connectivity and Euler number.

Some of the above measures have obvious meanings. The others will be described briefly below in the context of two-dimensional images.

Elongation

-- sometimes called eccentricity. This is the ratio of the maximum length of line or chord that spans the region to the minimum length chord. We can also define this in terms of moments as we will see shortly.

Compactness

-- this is the ratio of the square of the perimeter to the area of the region.

Moments of Inertia

-- the ijth discrete central moment 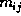of a region is defined by

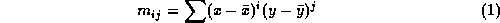
where the sums are taken over all points (x,y) contained within the region and 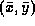is the centre of gravity of the region:

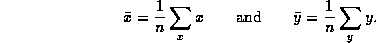
Note that, n, the total number of points contained in the region, is a measure of its area.

We can form seven new moments from the central moments that are invariant to changes of position, scale and orientation of the object represented by the region (invariants will be discussed below shortly), although these new moments are not invariant under perspective projection. For moments of order up to three, these are:
 

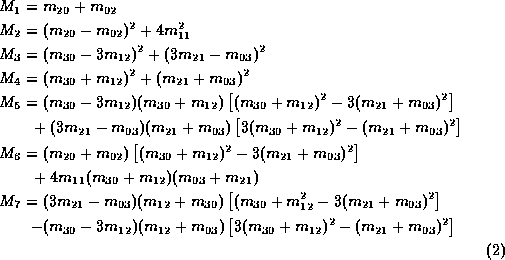
We can also define eccentricity using moments  as

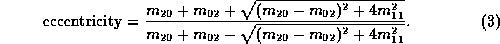
We can also find principal axes of inertia that define a natural coordinate system for a region. Let be given by

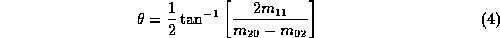
We will get two values for 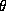which are 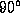apart. The pair of lines which make an angle 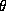with the x axis passing through the centre of gravity of the region define a pair of principal axes which are generally aligned along what would intuitively be called the length and width of the region.

Connectivity

-- the number of neighbouring features adjoining the region.

Euler Number

-- for a single region, one minus the number of holes in that region. The Euler number for a set of connected regions can be calculated as the number of regions minus the number of holes.

Most of these statistical measures may be useful in helping to control image reasoning and recognition, even if they are not sufficient for reasoning or recognition by themselves.

However, these measures are very cheap to calculate as byproducts of the segmentation strategies detailed, especially region growing. Consequently, when these measures are used in conjunction with other reliably extracted features, they can help to improve recognition techniques by constraining the search space for matches between image and object features.

Invariant Measures

Several of the statistical measures we have met are invariant measures, which is to say that the value of the measure does not vary with, for example, the position of the region in the image, or perhaps its orientation or scale.

This is clearly a good property as we cannot guarantee viewing an object from identical viewpoints.

Thus, while the centre of gravity of a region obviously varies with its position, its area does not. While area does vary with scale (and thus closeness of the camera to the object, for example), compactness as defined above is invariant with respect to scale as well as position and orientation.

Other invariant measures are:

• Descriptions of surface curvature -- Gaussian curvature and mean curvature are invariant with respect to rotation and translation of a surface.
• Moments of inertia (Eqn. 2)

  are invariant with respect to scaling, rotation and translation.

• Eccentricity is invariant with respect to scaling, rotation and translation.
• Fourier Transforms are rotation invariant. We can use the Fourier transform to compute Fourier descriptors of an object which are invariant with respect to position and orientation.