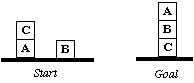
Above method may fail to give a good solution. Consider:
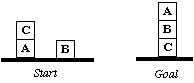
Fig. 25 Sussman's Anomaly
The start state is given by:
ON(C, A) ![]() ONTABLE(A)
ONTABLE(A) ![]() ONTABLE(B)
ONTABLE(B) ![]() ARMEMPTY
ARMEMPTY
The goal by:
ON(A,B) ![]() ON(B,C)
ON(B,C)
This immediately leads to two approaches as given below
ON(A,B)ON(B,C)
ON(A,B)
ON(B,C)
ON(B,C)ON(A,B)
ON(A,B)
ON(B,C)
Choosing path 1 and trying to get block A on block B leads to the goal stack:
ON(C,A)CLEAR(C)
ARMEMPTY
ON(C,A)
CLEAR(C)
ARMEMPTY
UNSTACK(C,A)
ARMEMPTY
CLEAR(A)
ARMEMPTY
PICKUP(A)
CLEAR(B)
HOLDING(A)
STACK(A,B)
ON(B,C)
ON(A,B)
ON(B,C)
This achieves block A on block Bwhich was produced by putting block C on the table.
The sequence of operators is
Working on the next goal of ON(B,C) requires block B to be cleared so that it can be stacked on block C. Unfortunately we need to unstack block A which we just did. Thus the list of operators becomes
To get to the state that block A is not on block B two extra operations are needed:
Analysing this sequence we observe that
So a more efficient scheme is:
To produce in all such cases this efficient scheme where this interaction between the goals requires more sophisticated techniques which will be considered in the next lecture.