Goal Stack Planning

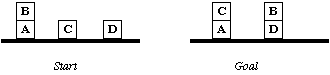
Basic Idea to handle interactive compound goals uses goal stacks, Here the stack contains :

• goals,
• operators -- ADD, DELETE and PREREQUISITE lists
• a database maintaining the current situation for each operator used.

Consider the following where wish to proceed from the start to goal state.

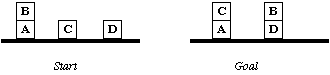
Fig. 24 Goal Stack Planning Example

We can describe the start state:

ON(B, A) ONTABLE(A) ONTABLE(C) ONTABLE(D) ARMEMPTY

and goal state:

ON(C, A) ON(B,D) ONTABLE(A) ONTABLE(D)

• Initially the goal stack is the goal state.
• We then split the problem into four subproblems
• Two are solved as they already are true in the initial state -- ONTABLE(A), ONTABLE(D).

• With the other two -- there are two ways to proceed:

  1.     ON(C,A)
     
     			ON(B,D)
     
     			ON(C,A)   ON(B,D)
     
     		     ONTABLE(A)  
     ONTABLE(D)
     
     

  2.     ON(B,D)
     
     			ON(C,A)
     
     			ON(C,A)   ON(B,D)
     
     		     ONTABLE(A)  
     ONTABLE(D)
     
     

The method is to

• Investigate the first node on the stack ie the top goal.
• If a sequence of operators is found that satisfies this goal it is removed and the next goal is attempted.
• This continues until the goal state is empty.

Consider alternative 1 above further:

• The first goal ON(C,A) is not true and the only operator that would make it true is STACK (C,A) which replaces ON(C,A) giving:

      B<>STACK (C,A)
  
  			ON(B,D)
  
  			ON(C,A)   ON(B,D)
  
  		     ONTABLE(A)  
  ONTABLE(D)
  
  

• STACK has prerequisites that must be met which means that block A is clear and the arm is holding block C. So we must do:

      B<>CLEAR(A)
  
  			HOLDING(C)
  
  		 CLEAR(A)  HOLDING(C)
  
  			STACK (C,A)
  
  			ON(B,D)
  
  			ON(C,A)   ON(B,D)
  
  		     ONTABLE(A)  
  ONTABLE(D)
  
  

• Now top goal is false and can only be made true by unstacking B. This leads to:

      B<>ON(B,A)
  
  			CLEAR(B) 
  
  			ARMEMPTY 
  
  			ON(B,A)   CLEAR(B)
  
  		     ARMEMPTY
  
  			UNSTACK(B,A)
  
  			HOLDING(C)
  
  			CLEAR(A)  HOLDING(C)
  
  		  
  

• Now the first goal is true, the second is universally true, and the arm is empty. Thus all top three goals are true means that we can apply the operator UNSTACK(B,A) as all prerequisites are met. This gives us the first node in database

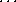
  ONTABLE(A) ONTABLE(C) ONTABLE(D) HOLDING(C) CLEAR(A)

• Note as a future reference of the use of UNSTACK(B,A) that HOLDING(B) is true as well as CLEAR(A)
• The goal stack becomes

      HOLDING(C)
  
  		 	CLEAR(A)  HOLDING(C)
  
  			STACK (C,A)
  
  			ON(B,D)
  
  			ON(C,A)   ON(B,D)   ONTABLE(A)
  
  		     ONTABLE(D)
  
  

• There are two ways we can achieve HOLDING(C) by using the operators PICKUP(C) or UNSTACK(C,x) where x is an unspecified block. This leads to two alternative paths:

  1.  ON(C, x)
     
     	CLEAR(C)
     
     ARMEMPTY
     
     ON(C, x)  CLEAR(C)
     
          ARMEMPTY
     
     UNSTACK(C,x)
     
     	CLEAR(A)  HOLDING(C)
     
     	STACK (C,A)
     
     	ON(B,D)
     
     	ON(C,A)   ON(B,D)   ONTABLE(A)
     
         
     ONTABLE(D)
     
     

1

1.  ONTABLE(C)
   
   	CLEAR(C)
   
   ARMEMPTY
   
   ONTABLE(C)  CLEAR(C)
   
        ARMEMPTY
   
   PICKUP(C)
   
   	CLEAR(A)  HOLDING(C)
   
   	STACK (C,A)
   
   	ON(B,D)
   
   	ON(C,A)   ON(B,D)   ONTABLE(A)
   
       
   ONTABLE(D)
   
   

In this first route we can see three references to some block, x and these must refer to the same block, although in the search it is conceivable several blocks will become temporarily attached. Hence the binding of variables to blocks must be recorded. Investigating further we need to satisfy the first goal and this requires stacking C on some block which is clear.

    CLEAR(x)

			HOLDING(C)

			CLEAR(x)  HOLDING(C)

			STACK (C, x)

			CLEAR(C)

			ARMEMPTY

			 

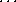
We now notice that one of the goals created is HOLDING(C) which was the goal we were trying to achieve by applying UNSTACK(C, some block) in this case and PICKUP(C) in the other approach. So it would appear that we have added new goals and not made progress and in terms of the A* algorithm it seems best to try the other approach.

So looking at the second approach

• We can see that the first goal is achieved block C is on the table.
• The second goal is also achieved block C is clear.
• Remember that HOLDING(B) is still true which means that the arm is not empty. This can be achieved by placing B on the table or planting it on block D if it is clear.
• Lookahead could be used here to compare the ADD lists of the competing operators with the goals in the goal stack and there is a match with ON(B,D) which is satisfied by STACK (B,D). This also binds some block to block D.
• Applying STACK (B,D) generates extra goals CLEAR(D) and HOLDING(B)

The new goal stack becomes;

    CLEAR(D)

		 HOLDING(B)

		 	CLEAR(D)   HOLDING(B)

		 STACK (B, D)

		 ONTABLE(C)  CLEAR(C)  ARMEMPTY

		 	PICKUP(C)

			 

• At this point the top goal is true and the next and thus the combined goal leading to the application of STACK (B,D), which means that the world model becomes

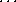
  ONTABLE(A) ONTABLE(C) ONTABLE(D) ON(B,D) ARMEMPTY

• This means that we can perform PICKUP(C) and then STACK (C,A)
• Now coming to the goal ON(B,D) we realise that this has already been achieved and checking the final goal we derive the following plan
  1. UNSTACK(B,A)
  2. STACK (B,D)
  3. PICKUP(C)
  4. STACK (C,A)

This method produces a plan using good Artificial Intelligence techniques such as heuristics to find matching goals and the A* algorithm to detect unpromising paths which can be discarded.

 
• Sussman Anomaly (1975)