Next: Differential Encoding
Up: Source Coding Techniques
Previous: Relationship between DCT and
The discrete cosine transform (DCT) helps separate the image into parts
(or spectral sub-bands) of differing importance (with respect to the
image's visual quality). The DCT is similar to the discrete Fourier
transform: it transforms a signal or image from the spatial domain to the
frequency domain (Fig 7.8).
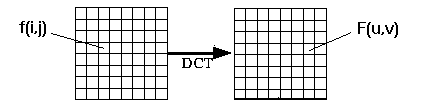
DCT Encoding
The general equation for a 1D (N data items) DCT is defined by the
following equation:
![\begin{displaymath}
F(u) = \left(\frac{2}{N}\right)^{\frac{1}{2}} \sum_{i=0}^{N-1}
\Lambda(i).cos\left[
\frac{\pi.u}{2.N}(2i+1)
\right]f(i)\end{displaymath}](img26.gif)
and the corresponding inverse 1D DCT transform is simple
F-1(u), i.e.:
where
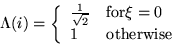
The general equation for a 2D (N by M image) DCT is defined by the
following equation:
![\begin{displaymath}
F(u,v) = \left(\frac{2}{N}\right)^{\frac{1}{2}}
\left(\frac{...
...}(2i+1)
\right]cos\left[ \frac{\pi.v}{2.M}(2j+1) \right].f(i,j)\end{displaymath}](img28.gif)
and the corresponding inverse 2D DCT transform is simple
F-1(u,v), i.e.:
where
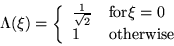
The basic operation of the DCT is as follows:
- The input image is N by M;
- f(i,j) is
the intensity of the pixel in row i and column j;
- F(u,v) is the DCT
coefficient in row k1 and column k2 of the DCT matrix.
- For most images, much of the signal energy lies at low
frequencies; these appear in the upper left corner of the DCT.
- Compression is achieved since the
lower right values represent higher frequencies, and are often small -
small enough to be neglected with little visible distortion.
- The DCT input
is an 8 by 8 array of integers. This array contains each pixel's gray
scale level;
- 8 bit pixels have levels from 0 to 255.
- Therefore an 8 point DCT would be:
where
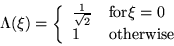
Question: What is F[0,0]?
answer: They define DC and AC
components.
- The output
array of DCT coefficients contains integers; these can range from -1024
to 1023.
- It is computationally easier to implement and more efficient
to regard the DCT as a set of basis functions which given a known
input array size (8 x 8) can be precomputed and stored. This involves
simply computing values for a convolution mask (8 x8 window) that get
applied (summ values x pixelthe window overlap with image apply window
accros all rows/columns of image). The values as simply calculated from
the DCT formula. The 64 (8 x 8) DCT basis functions are illustrated in
Fig 7.9.

DCT basis functions
- Why DCT not FFT?
DCT is similar to the Fast Fourier Transform (FFT), but can approximate
lines well with fewer coefficients (Fig 7.10)
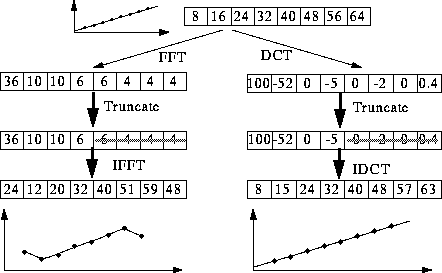
DCT/FFT Comparison
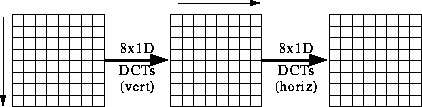
- Computing the 2D DCT



Next: Differential Encoding
Up: Source Coding Techniques
Previous: Relationship between DCT and
Dave Marshall
10/4/2001


![\begin{displaymath}
F(u) = \left(\frac{2}{N}\right)^{\frac{1}{2}} \sum_{i=0}^{N-1}
\Lambda(i).cos\left[
\frac{\pi.u}{2.N}(2i+1)
\right]f(i)\end{displaymath}](img26.gif)
![]()
![\begin{displaymath}
F(u,v) = \left(\frac{2}{N}\right)^{\frac{1}{2}}
\left(\frac{...
...}(2i+1)
\right]cos\left[ \frac{\pi.v}{2.M}(2j+1) \right].f(i,j)\end{displaymath}](img28.gif)
![]()
![]()