The basic Huffman algorithm has been extended, for the following reasons:
(a) The previous algorithms require the statistical knowledge which is often not available (e.g., live audio, video).
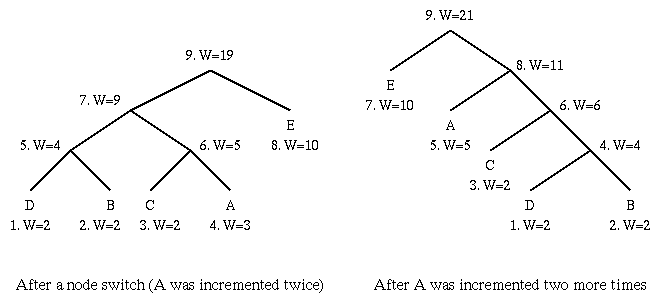
(b) Even when it is available, it could be a heavy overhead especially when many tables had to be sent when a non-order0 model is used, i.e. taking into account the impact of the previous symbol to the probability of the current symbol (e.g., "qu" often come together, ...).
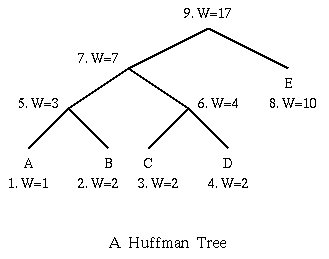
The solution is to use adaptive algorithms. As an example, the Adaptive Huffman Coding is examined below. The idea is however applicable to other adaptive compression algorithms.
ENCODER DECODER
------- -------
Initialize_model(); Initialize_model();
while ((c = getc (input)) != eof) while ((c = decode (input)) != eof)
{ {
encode (c, output); putc (c, output);
update_model (c); update_model (c);
} }
}