Huffman Coding

Huffman coding is based on the frequency of occurance of a data item (pixel in images). The principle is to use a lower number of bits to encode the data that occurs more frequently. Codes are stored in a Code Book which may be constructed for each image or a set of images. In all cases the code book plus encoded data must be transmitted to enable decoding.

The Huffman algorithm is now briefly summarised:

• A bottom-up approach

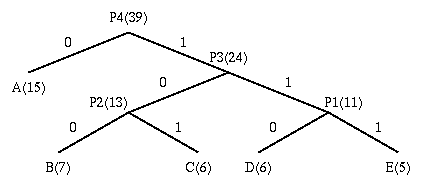
1. Initialization: Put all nodes in an OPEN list, keep it sorted at all times (e.g., ABCDE).

2. Repeat until the OPEN list has only one node left:

(a) From OPEN pick two nodes having the lowest frequencies/probabilities, create a parent node of them.

(b) Assign the sum of the children's frequencies/probabilities to the parent node and insert it into OPEN.

(c) Assign code 0, 1 to the two branches of the tree, and delete the children from OPEN.

      Symbol   Count   log(1/p)     Code     Subtotal (# of bits)
     ------   -----   --------   ---------  --------------------
        A      15       1.38          0             15
        B       7       2.48        100             21
        C       6       2.70        101             18
        D       6       2.70        110             18
        E       5       2.96        111             15
                                 TOTAL (# of bits): 87

The following points are worth noting about the above algorithm:

• Decoding for the above two algorithms is trivial as long as the coding table (the statistics) is sent before the data. (There is a bit overhead for sending this, negligible if the data file is big.)

• Unique Prefix Property: no code is a prefix to any other code (all symbols are at the leaf nodes) -> great for decoder, unambiguous.

• If prior statistics are available and accurate, then Huffman coding is very good.

In the above example:

Number of bits needed for Huffman Coding is: 87 / 39 = 2.23