
Complex decorative reliefs are often added to CAD models in such application areas as sign-making, packaging, and ceramics to make product designs more interesting, more characteristic of the company, or of higher intrinsic value.
New reliefs can be created from 2D artwork using software such as Delcam’s ArtCAM, or can be hand-crafted, typically on a planar surface, and reverse engineered using a 3D scanner. Unfortunately, extraction of the relief from the scan of a physical part is only possible when the relief is lying on a planar surface. As in general such reliefs lie on freeform surfaces, reverse engineering methods are needed to separate the relief from the non-planar background, and to assist in the application of the relief to a different base surface.
This project aims to device mathematical methods and algorithms for the reverse engineering and reapplication of reliefs. The work concerns separating scan points belonging to the relief from the background, identifying single units of repeating relief patterns, fitting the background surface and flattening the relief’s underlying surface.
Some relief objects are shown below:

|
| A duck relief |

|
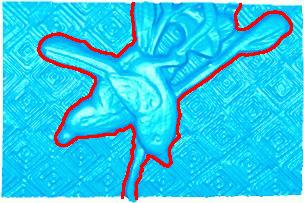
| Bird relief on a textured background |

|
| Cyclic Reliefs |
More details are given in:
 |
|
 |
|
 |
|
 |
|
return to Paul Rosin's homepage