Searching Graphs

Consider the following :

  
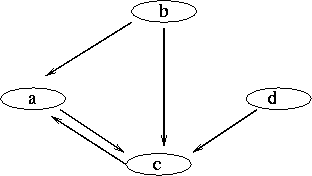
Figure 2: A graph

• The graph is obtained by linking nodes via edges
• A directed graph is one where the edges also have direction (usually called arcs)

The graph above can be described, by simply stating the interconnections :

 
arc(a,c).
arc(a,b).
arc(c,a).
arc(c,b).
arc(c,d).

Also, we can define a simple procedure which evaluates to true if a path between two given nodes can be found :

path(X,Y) :-
 arc(X,Y).

path(X,Y) :-
 arc(X,Z),
 path(X,Z).

• What does this definition tell us?
• First rule says that a path between X and Y exists, if an arc can be found between X and Y in the database
• Second rule says that a path exists between X and Y, if a series of arcs (intermediate nodes Z) can be obtained from X to Y
• BUT

If issued the query :

path(a,d)

• Prolog goes into an infinite loop, because of the presence of the cycle between a and c, hence we have to change our definition to overcome this problem
• So how do we do this ?

path(X,Y) :-
 path(X,Y, []).

path(X,Y,_) :-
 arc(X,Y).

path(X,Y,Trail) :- 
 arc(X,Z),
 not(member(Z,Trail)),
 path(Z,Y,[X|Trail]).

what does this do ?

• In the first case X is directly connected to Y by a single arc - so the Trail list is empty
• This is defined by the first two rules. The use of the anonymous variable suggests that whatever the Trail, if a direct arc exists - thats fine
• Third rule uses an indirection, by considering an intermediate node, labelled Z - and tries to determine if Z has been examined already or not
• Notice the use of member definition along with a list definition. The last path statement is used to say that X has already been examined
• This prevents the occurrence of cycles and overcomes the problems with the first definition

More complex arithmetic manipulation of lists via recursion

squares([],[]).

squares([ N| Tail],[S | Stail]) :-
 S is N*N,
 squares(Tail, Stail).

• A procedure for performing a transformation on all elements of a list
• Gives the square of numbers in a given list
• First rule : square of an empty list is an empty list
• Second rule : Input composed of two lists, with each list composed of a head (N for first list and S for second list), and tail (Tail for first list, and Stail for second list)
• Take the first element of first list and square it
• First element of second list becomes that result
• Remove the first element from both lists (as that has now been squared), and perform the same on the remainder of the list i.e. the tail
• Repeat the process until an empty list is obtained