Neural models of arbitrary chaotic systems

Abstract. This paper proposes a simple methodology to construct an iterative neural network which mimics a given chaotic time series. The methodology uses the Gamma test to identify a suitable (possibly irregular) embedding of the chaotic time series from which a one step predictive model may be constructed. A one-step predictive model is then constructed as a feedforward neural network trained using the BFGS method. This network is then iterated to produce a close approximation to the original chaotic dynamics.

We then show how the chaotic dynamics may be stabilized using time-delayed feedback. Delayed feedback is an attractive method of control because it has a very low computational overhead and is easy to integrate into hardware systems. It is also a plausible method for stabilization in biological neural systems.

Using delayed feedback control, which is activated in the presence of a stimulus, such networks can behave as an associative memory, in which the act of recognition corresponds to stabilization onto an unstable periodic orbit. Surprisingly we find that the response of such systems is remarkably robust in the presence of noise. We briefly investigate the stability of the proposed control method and show that whilst the control/synchronisation methods are not always stable in the classical sense they may instead be probabilistically locally stable.

We also show how two independent copies of such a chaotic iterative network may be synchronized using variations of the delayed feedback method. Although less biologically plausible, these techniques may have interesting applications in secure communications.

Keywords: Chaos, Neural Networks, Chaos control, Model identification, synchronization, probabilistic local stability, Gamma test.

This HTML file is a supplement to the paper described and referenced above. It contains the detailed descriptions and results of the various experiments referred to in the paper.

1 Probabilistic local stability

Little theoretical analysis is available for the Pyragas method of continuous delayed feedback control, let alone for the discrete form of the method used here. However, [Oliveira 1998] also contained a suggestive discussion of the local stability properties of the method used there. For both the HŽnon map and a chaotic neural network it was shown that whilst the synchronization control method used by [Oliveira 1998] was not locally stable it was nevertheless probabilistically locally stable.

We illustrate here one example of a similar empirical analysis for the method of stabilization proposed in the case where no external stimulus is present.(Similar results can be obtained for the other examples.)

Using the Lorenz system (*) with

= 10, r = 28 and b = 8/3, we provide a simple delayed feedback as in the original Pyragas' continuous feedback on the y variable (assuming the system is time dependent on variable t),

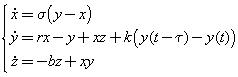where the feedback parameters are

= 1, and k = 0.99. We then generate random initial states

= (x, y, z) for the variable x, y and z in [-50, 50] to study the dynamics. In most cases, the system fairly quickly stabilizes onto one of the two embedded unstable fixed points of the original attractor,

_F1 = (-8.485281, -8.485281, 27) and

_F2 = (8.485281, 8.485281, 27), depending on the initial start states when the control is switched on. The control signal k(y(t-

) - y(t)) is small once the system is on either of these fixed point states. Although a carefully examination will show that the signal only becomes very small - it does not actually become zero. The initial states for all variables are randomly generated in the range [-50, 50], which is large compared with the attractor region for some of them. We notice that within this range there exists a small region in which the system is trapped and "stabilized" onto a periodic orbit which is not the desired control result. It is undesirable because t

he control signal is large. Fig 1 and Fig 2 show the histograms for

(t) = min(|(t) - _F1|, |(t) - _F2|), the minimum of the Euclidean distance of the stabilized state from the two fixed points. We see that, with the exception of the trapped region, for

> 0,

as t

, i.e.

(t) tends to zero in probability. This illustrates the probabilistically local stability of this controlled system.

However, we should distinguish between probabilistically local stability for simple stabilization of the system and for synchronization of two identical chaotic systems. For other similar synchronization methods the idea of probabilistic local stability is not required, stability can be directly linked to the choice of the parameter k and this in turn may relate to the idea of a blowout bifurcation [Ashwin 1996, Nagai 1997], especially if the system is discrete.

2 Examples of model construction

The networks used the sigmoidal function

, where the temperature T = 0.833 and the scale factor s_F = 1.5, as the output function, where the activation x is given by

where a_ij is the weight from node j to node i and x_j is the output of node j. The networks were trained by using the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm [Fletcher 1987] with a slightly modified line search procedure which proved more effective for large training sets.

Using an initial conditions (x₀, y₀) = (1.4, 0), we generate a time series of 1000 data points using this map. A typical HŽnon time series is shown in Fig 3. Using the technique from [Sano 1985] on the x time series, the Lyapunov exponents were estimated to be {0.42, -1.58}.

Suppose we examine the prospect of trying to predict x(n) using the last 6 values. Since 2⁶ - 1 = 63 it is no problem to do a full embedding search. We find that the best embedding (i.e. the embedding with smallest |

|) is 101111, which means that we predict x(n) using x(n-1), x(n-2), x(n-3), x(n-4) and x(n-6). It is interesting to note that the full embedding search obtained most of the best 8 embeddings including the past values x(n-1) and x(n-2), see Table 1. Why is this? In the original map, the system value depends x(n) on the past values x(n-1) and x(n-2), as the software discovered. On this basis we generate the results in Table 2 and Fig 4 - Fig 5. Note that SE in Table 2 is the standard error, the usual goodness of fit applied to the regression line as in Fig 4. If this number is close to zero we have more confidence in the value of the Gamma statistic as an estimate for the noise variance on the given output. The value V_ratio is defined as

/Var(output) and represents a standardized measure of the Gamma statistic which enables a judgement to be formed, independently of the output range, as to how well the output can be modeled by a smooth function. In comparing different outputs, or outputs from different data sets, V_ratio is a useful quantity to examine, because it is independent of the output range. A V_ratio close to zero indicates a high degree of predictability ( by a smooth model) of the particular output. If the V_ratio is close to one the output is equivalent to random noise as far as a smooth model is concerned.

A neural network with 5 inputs, two hidden layers having 8 neurons in the first one and 5 neurons in the second one and 1 output neuron (5-8-5-1) was trained using M = 800 data points to a MSError of 2.92514×10^-5 which is comparable with the Gamma statistic. The plot of x(n+1) against x(n) in Fig 6 shows the original attractor constructed from the training data. Fig 7 shows the analogous result obtained by iterating the trained neural network. Using a regular embedding of the 2 past values of the network output, together with [Sano 1985] technique, we estimated the Lyapunov exponents to be {0.41, -1.65} to 2 decimal places. We further tested the network by predicting the outputs on 100 unseen data from the map and we got a MSError of 4.15335×10^-5 from the network, a respectable performance broadly in line with the statistic given in Table 2.

The Mackey-Glass equation is a time delayed differential equation which produces a chaotically evolving continuous dynamic system. The version used to generate the data is given by

We integrated the equation over t

[0, 8000] with the initial condition x(t) = 2. No noise was added. The graph of the function over t

[0, 1000] is given in Fig 8. The Lyapunov exponents from the training time series are {0.001, -0.006, -0.027} to 3 decimal places using the technique from [Sano 1985].

The Mackey-Glass time series data was created by writing out the values of x(t) at t = 10, 20, 30, ..., 8000 (

t = 10) giving 800 data points of a chaotic time series. Given a reasonable amount of data, predicting a chaotic time series a small time ahead is usually not too difficult. The problem is to predict a long way ahead. Here t = 10 is a modest time ahead. If smaller time steps are taken then using several previous values to predict x(t) we find that the resulting

is extremely small, indicating that predicting this function small steps ahead is very easy.

Suppose we examine the prospect of trying to predict x(t) using the last 6 values. Since 2⁶ - 1 = 63 it is no problem to do a full embedding search. We find that the best embedding (i.e. the embedding with smallest |

|) is 111100, which means that we predict x(t) using x(t-3.

t), x(t-4.t), x(t-5.

t) and x(t-6.

t). On this basis we generate the results in Table 4 and Fig 9 - Fig 10.

It is interesting to note that the full embedding search obtained the best model by omitting x(t-1.t) and x(t-2.

t). Why is this? In the original time delay equation the value x(t) depends on the value x(t-30) but x(t-10) and x(t-20) are not needed at all, as the software discovered.

The embedding 111100 provides a four input/one output set of I/O pairs. The low noise level

0.0003, combined with the rapid fall off of the M-test graph (Fig 10), and V_ratio

0.004 indicates the existence of a reasonably accurate smooth model. The regression line fit is good with SE

0.0002. The slope A

0.298 is low enough to suggest a fairly simple nonlinear model. Taken together these are clear indicators that it should be quite straightforward to construct a predictive model using around 800 data points with an expected MSE around 0.0003. The scatter plot of Fig 9 contains the typical more or less blank wedge in the lower small

region, which also supports the conclusion.

A neural network with 4 inputs, two hidden layers with eight neurons each and one output neuron (4-8-8-1) was trained using M = 800 data points to a MSError of 0.000329877 which is comparable with the Gamma statistic. The plot of x(n+1) against x(n) in Fig 11 shows the original attractor constructed from the training data. Fig 12 shows the analogous result obtained by iterating the trained neural network. Using 100 unseen samples with the same sampling time of

t = 10 from the system as test data, we calculated the error of the network on this test data to be 0.000401095 which is again in line with the

statistic of Table 4. Using the technique in [Sano 1985] with an embedding of dimension 3 on 800 data points generated by the network, we estimated the Lyapunov exponents to be {0.059, -0.044, -0.239} to 3 decimal places. We should note that using such a short time series may produce inaccurate values of the true Lyapunov exponents but applying this technique to the training data facilitates a direct comparison between the trained neural network and the training data.

where the parameters

= 10, r = 28 and b = 8/3 producing a chaotic attractor. We estimated the Lyapunov exponents of this system to be {0.90, -0.01, -14.55} to 2 decimal places using the technique from [Parker1992, p.80] by integrating the whole system. We sampled the x variable of these equations at intervals of

t = 0.1 to generate 10,000 training data points. We then applied the technique from [Sano 1985] to estimate the Lyapunov exponents based on this sampled time series, with an embedding of dimension 3, to be {1.27,-0.06, -12.34} to 2 decimal places. Although estimating the Lyapunov exponents in this way seems to be less accurate the approach does provide a means for comparing the network dynamics with only one output with the original system dynamics, using the sampled time series.

Suppose we examine the prospect of trying to predict x(n) using the last 10 values. Since 2¹⁰ - 1 = 1023 it is no problem to do a full embedding search.

Fig 13 shows the a histogram of all 1023 Gamma values - we call this an embedding histogram. Embedding histograms are often a useful diagnostic tool giving clues to the underlying dynamics or lack of it. for example, a bell shaped embedding histogram is often indicative of a time series closer to a random walk than a dynamical system, whereas a multimodal or a sharply decaying histogram (such as Fig 13) is usually indicative of strong underlying dynamics.

We find that the best embedding (i.e. the embedding with smallest |

|) is 0101111011. The first 8 best embeddings found are shown in Table 5. On this basis we generate the results in Table 6 and Fig 14 - Fig 15.

A 7-5-10-1 neural network was trained using M = 10,000 data points to a MSError of 5.91933×10^-5, which is comparable with the Gamma statistic.

The plot of x(n+1) against x(n) in Fig 16 shows the original attractor constructed from the training data. Fig 17 shows the analogous result obtained by iterating the trained neural network. The network Lyapunov exponents were estimated, using an embedding of dimension 3 of the network output (a time series of 10000 data) together with the technique in [Sano 1985], to be {0.12, -0.00, -1.16} in 2 decimal places. The results seem to be about 10 times smaller than the estimates for the original time series. This is because each iteration of the network is equivalent to an interval of

t = 0.1 for the original Lorenz system, therefore we expect the Lyapunov exponents to be 10 times smaller. Using 500 unseen sampled data to form our test data set, we tested the network and this gave a MSError of 3.09418×10^-4, which indicates that the network seems to model the system fairly well.

Fig 16 Phase space of x(n+1) against x(n) of the Lorenz x time series data.

Fig 17 Phase space of the output x(n+1) against x(n) for the iterated Lorenz 7-5-10-1 network.

Another example of a chaotic neural network is constructed and trained on a time series of the variable w of the hyperchaotic Chua circuit system defined by:

where f(t) = b t + (1/2) (a-b) (|t+1|-|t-1|),

= 10,

= 17.87, a = -1.27 and b = -0.68. In this experiment, the parameter k is chosen to be 0.5, which is within the required range (0, 1.17) for this system to exhibit chaotic behavior. This system is numerically integrated for t

[0, 900] with initial conditions x = 0.1, y = z = v = w = 0 and u = 0.011. The continuous time series w, as in Fig 18, is then sampled at time every

t = 0.25 time units so that a discrete time series of 3600 samples is obtained as the training data for constructing the chaotic neural network. Using the technique from [Sano 1985] on this sampled time series, approximate estimates for the Lyapunov exponents were found to be {1.03, 0.42, -0.05, -0.79, -2.14, -3.72}. Based on the time series samples for w we can reconstruct the chaotic attractor as in Fig 19.

We examine the prospect of trying to predict x(n) using the last 10 values. Since 2¹⁰ - 1 = 1023 it is no great problem to do a full embedding search. Fig 20 shows the embedding histogram with a sharply decaying shape suggesting strong underlying dynamics. We find that the best embedding (i.e. the embedding with smallest |

|) is 0110000111. The first best 8 embeddings found are listed in Table 7. On this basis we generate the results in Table 8 and Fig 21 - Fig 22.

A 5-10-10-1 neural network was trained on M = 3500 data points to a MSError of 7.31100×10^-6, which is comparable with the Gamma statistic. Fig 23 shows the plot against time of the output of the trained neural network when iterated and can be compared with Fig 18 for the original time series for w.

The plot of w(n+1) against w(n) in Fig 19 shows the original attractor constructed from the training data. This can be compared with Fig 24, which shows the analogous result obtained by iterating the trained neural network. Using the network output with a regular embedding of dimension 6 together with the technique from [Sano 1985], the Lyapunov exponents of the system are approximately estimated to be {0.14, 0.06, -0.02, -0.16, -0.43, -0.78} in 2 decimal places and taking each network iteration as 1 time unit. Therefore, these Lyapunov exponents should be one quarter of the Lyapunov exponents estimated on the training data, which have a sampling time of

t = 0.25 time unit. The test MSError on 300 unseen data sampled from the original system with the same sampling time is about 5.40465×10^-6.

3. Delayed feedback control

There follows a gallery of different responses of the systems using different settings of controls and external stimulation. The response signals of the system can be observed at the output x(n) of the feedforward neural network module or the "observation points" on the delay lines x(n-1) …, x(n-d), as indicated in Fig 25. Due to the complexity of these neural systems, of course, not all possible settings are tried and presented.

Fig 25 A general scheme for constructing a stimulus-response chaotic recurrent neural network: the chaotic "delayed" network is trained on suitable input-output data constructed from a chaotic time series; a delayed feedback control is applied to each input line; entry points for external stimulus are suggested, with a switch signal to activate the control module during external stimulation; signals on the delay lines or output can be observed at the "observation points".

We use

= 2 and k = 0.441628 for our control parameters on all the possible feedback control lines. The control is applied to the delayed feedback line x(n-6). Without any external stimulation and using only a single control delayed feedback, the network quickly produces a stabilized response as shown in Fig 26 with the corresponding control signal shown in Fig 27. Notice that the control signal is very small during the stabilized behavior. Under external stimulation with varying strength the network is still stabilized, but with a variety of new periodic behaviors as shown in Fig 28. The corresponding control signal is still small (see Fig 29).

Fig 26 Response signal on x(n-6) with control signal activated on x(n-6) using k = 0.441628,

= 2 and without external stimulation after first 10 transient iterations. After n = 1000 iterations, the control is switched off.

Fig 27 The control signal corresponding to the delayed feedback control shown in Fig 26. Note that the control signal becomes small.

Fig 28 Response signals on network output x(n), with control signal activated on x(n-6) using k = 0.441628,

= 2 and with constant external stimulation s_n added to x(n-6), where s_n varies from -1.5 to 1.5 in steps of 0.1 at each 500 iterative steps (indicated by the change of Hue of the plot points) after 20 initial transient steps.

Fig 29 The control signal corresponding to the delayed feedback control shown in Fig 28. Note that the control signal becomes small even when the network is under changing external stimulation.

For this system we then investigated the response of the system when the sensory input was perturbed by additive Gaussian noise r with Mean[r] = 0 and standard deviation SD[r] =

. Using the experimental setup as in Fig 28, the external stimulus was perturbed at each iteration step by adding a Gaussian noise r with standard deviation

, i.e. having an external stimulus s_n+r. This experiment was repeated for different

, where

was varied from

= 0.05 to

= 0.3, a high noise standard deviation with respect to the external stimulus range of -1.5 to 1.5. The result for

= 0.05 is shown in Fig 30 and Fig 31. Surprisingly, the response signal almost stays the same but the control signal is not small at all. The results for

= 0.15 and

= 0.3 are in Fig 32 and Fig 33 respectively. As illustrated in these figures, the system dynamics remain essentially unchanged, although as one might expect the response signal becomes progressively "blurred" as the noise level increases. Similar results can be obtained for the other examples.

Fig 30 Response signals on network output x(n), with control setup same as in Fig 28 but with Gaussian noise r added to external stimulation, i.e. s_n+r, with

= 0.05, at each iteration step.

Fig 31 The control signal corresponding to the delayed feedback control shown in Fig 30.

Fig 32 Response signals on network output x(n), with control experiment setup same as in Fig 28 but with Gaussian noise r added to external stimulation, i.e. s_n+r, with

= 0.15, at each iteration step.

Fig 33 Response signals on network output x(n), with control experiment setup same as in Fig 28 but with Gaussian noise r added to external stimulation, i.e. s_n+r, with

= 0.3, at each iteration step.

We use

= 5 and k = 0.414144 for our control parameters on all the possible feedback control lines. The control is applied to the delayed feedback line x(n-6). Without any external stimulation and using only a single control delayed feedback, the network quickly produces a periodic response as shown in Fig 34.

Fig 34 Response signal on x(n-6) with control signal activated on x(n-6) using k = 0.414144,

= 5 and without external stimulation.

Fig 35 Response signals on network output x(n), with control signal activated on x(n-6) using k = 0.414144,

= 5 and with constant external stimulation s_n added to x(n-5), where s_n varies from -1 to 1 in steps of 0.05 at each 400 iterative steps (indicated by the change of Hue of the plot points) after 20 initial transient steps.

Fig 36 Response signal at network output x(n) with control signal activated on all delay lines using k = 0.414144,

= 5 and with external stimulation s_n added to x(n-6), where s_n varies from -1 to 1 in steps of 0.05 changing at every 500 iterative steps (indicated by the change of Hue of the plot points) after 20 initial transient steps.

Fig 37 Response signals on the network output x(n) with control signal activated on all delay lines using k = 0.414144,

= 5 and with external stimulation s_n⁽¹⁾ added to x(n-6), where s_n varies from -0.5 to 0.5 in increasing steps of 0.05, and s_n⁽²⁾ added to x(n-5), where s_n varies from 0.5 to -0.5 in decreasing steps of 0.05, changing at every 500 iterative steps (indicated by the change of Hue of the plot points) after 20 initial transient steps.

Fig 35 shows the signal on the output x(n) of the feedforward neural network module with the control signal on x(n-6) using k = 0.414144,

= 5 and with external stimulation s_n added to x(n-5). This simple combination using a single control line plus a stimulation on the delay line already produces a variety of dynamical behaviors, but when the external stimulus is high, the system appears to be chaotic. Using the same multiple control settings for all delay lines, the system can be stimulated on the delay line x(n-6) (just after the delay buffer) by a constant external signal s_n, where s_n varies from -1 to 1 in steps of 0.05 at every 500 iterations after the first 20 steps. The result of the signals on x(n) is shown in Fig 36 and exhibits very high period stabilized behaviors for some stimuli. Fig 37 illustrates another example using two different external stimulation signals at x(n-5) and x(n-6) and achieving a wide variety of periodic responses.

Using a simple delayed feedback on x(n-1) delay line with k = 0.0925242 and

= 2, this neural system can be stabilized onto a period 1 motion with a very small control signal, as shown in Fig 38 and Fig 39. The control is switched on at n = 1500 and then switched off at n = 3000. Notice that the system quickly stabilizes once the control is applied but it takes a longer time to return to a chaotic mode.

Fig 38 After the delayed feedback control on x(n-1) delay line, with k = 0.0925242 and

= 2, is switched on at time iteration 1500, the system dynamics quickly stabilizes onto a period 1. At iteration 3000 the control is switched off.

Fig 39 The corresponding control feedback signal for the delayed feedback control experiment on x(n-1) delay line, with k = 0.0925242 and

= 2 as in Fig 38.

Fig 40 Output x(n) with control signal activated on x(n-1) using k = 0.0925242,

= 2 and with constant external stimulation s_n added to x(n-1), where s_n varies from -1.5 to 1.5 in steps of 0.1 at each 2000 iterative steps (indicated by the change of Hue of the plot points) after 10 initial steps.

Fig 41 The corresponding control feedback signal activated on x(n-1) using k = 0.0925242 and

= 2 for the experiment on constant external stimulation s_n added to x(n-1) as in Fig 40.

Using delayed feedback control on the x(n-1) delay line with the same k and

, external stimulation s_n with varying strength is applied to the system the resulting output x(n) is shown in Fig 40. Various periodic motions as well as quasi-periodic motions can be seen. The corresponding control signal acting on x(n-1) during the external stimulation is shown in Fig 41. Many interesting periodic motions are achieved but not necessarily with very small control signals acting on the delayed feedback control lines.

Fig 42 shows a similar experiment result - the response signal x(n) - but this time multiple delayed control feedbacks are used. Under several and different simultaneous external signals, this neural system exhibits a different set of period behaviors

Fig 42 Output x(n) with multiple control signals activated on x(n-1), x(n-2) and x(n-4) using k = 0.0925242,

= 2 and with constant external stimulation s_n⁽¹⁾ added to x(n-1), where s_n⁽¹⁾ varies from -1.5 to 1.5 in steps of 0.1, s_n⁽²⁾ added to x(n-2), where s_n⁽²⁾ varies from 1.5 to -1.5 in steps of -0.1 and s_n⁽³⁾ added to x(n-4), where s_n⁽³⁾ = s_n⁽¹⁾, at each 2000 iterative steps (indicated by the change of Hue of the plot points) after 10 initial steps.

Again a simple delayed feedback can be applied to the delay line x(n-1) and using k = 0.485412 and

= 3, with no external stimulation, the system quickly stabilizes onto an embedded period 1 attractor, as in Fig 43, with only a very small control signal (Fig 44).

Instead, by varying

we notice that having

= 5 for the control on the delay line x(n-1) only causes the system to exhibiting high periodic response signal, although the acting control signal is not small. Under simple perturbation as in Fig 45, the system produces a richer variety of dynamics according to the size of the external stimulation. Under the same setup of the experiment, but with multiple delayed feedback control on delay lines x(n-1), x(n-8) and x(n-9) further shows that a different set of response signals can be produced, see Fig 46. Using the multiple delayed feedback control setup again, we can apply multiple external stimulation to the delay lines x(n-1), x(n-8) and x(n-9). The detail and the response of the output x(n) are shown in Fig 47.

Fig 43 After the delayed feedback control on x(n-1) delay line, with k = 0.485412 and

= 3, is switched on at n =2000, the system dynamics quickly stabilizes onto a period 1 orbit.

Fig 44 The control signal acting on the Hyperchaotic Chua network corresponding to Fig 43. Note that the control signal quickly becomes small after the control is switched on.

Fig 45 Output x(n) with control signal activated on x(n-1) using

= 5, k = 0.485412 and with constant external stimulation s_n added to x(n-1), where s_n varies from -1.5 to 1.5 in steps of 0.1 at each 800 iterative steps (indicated by the change of Hue of the plot points) after 20 initial steps.

Fig 46 Output x(n) with multiple control signals activated on x(n-1), x(n-8) and x(n-9) using

= 5, k = 0.485412 and with constant external stimulation s_n added to x(n-1), where s_n varies from -1.5 to 1.5 in steps of 0.1 at each 700 iterative steps (indicated by the change of Hue of the plot points) after 20 initial steps.

Fig 47 Output x(n) with multiple control signals activated on x(n-1), x(n-8) and x(n-9) using = 5, k = 0.485412 and with constant external stimulation s_n⁽¹⁾ added to x(n-1), where s_n⁽¹⁾ varies from -1.5 to 1.5 in steps of 0.1, s_n⁽²⁾ added to x(n-8), where s_n⁽²⁾ varies from 1.5 to -1.5 in steps of -0.1 and s_n⁽³⁾ added to x(n-9), where s_n⁽³⁾ = s_n⁽¹⁾, at each 700 iterative steps (indicated by the change of Hue of the plot points) after 20 initial steps.

4 Synchronization

We will now give experimental results for both synchronization methods (Method I in Fig 48 and Method II in Fig 49) and show how a suitable value for the feedback constant can be determined by examining the maximum Lyapunov exponent of the difference between the two systems.

Two HŽnon neural networks were synchronized using Method I with k = 0.8. The results can be seen in Fig 51. Similarly, the result for using synchronization Method II with k = -0.6 is shown in Fig 53. The graphs of maximum Lyapunov exponent against k averaged over 10 sets of initial conditions for the synchronization of two HŽnon networks using Method I and using Method II are shown in Fig 50 and Fig 52 respectively. Interestingly, the range for k to achieve synchronization using Method II is rather small.

Fig 50 Average maximum Lyapunov exponent against k for the synchronization of two HŽnon networks using method I.

Fig 51 Synchronization of two HŽnon networks with different initial conditions using method I with k = 0.8.

Fig 52 Average maximum Lyapunov exponent against k for the synchronization of two HŽnon networks using method II.

Fig 53 Synchronization of two HŽnon networks with different initial conditions using method II with k = -0.6.

Two Mackey-Glass Neural Networks were synchronized using Method I with k = 1.1. The results can bee seen in Fig 55. The graph of maximum Lyapunov exponent against k averaged over 10 sets of initial conditions for the synchronization of two Mackey-Glass networks using Method I is shown in Fig 54 . Fig 57 shows an attempt at synchronization of the two networks using Method II using k = 0.5, the minimum value as suggested by Fig 56, the graph of maximum Lyapunov exponent of the system difference against k. This was not a successful synchronization and this is suggested by the non-negative Lyapunov exponents within the range of k investigated in Fig 56.

Fig 54 Average maximum Lyapunov exponent against k for the synchronization of two Mackey-Glass networks using Method I.

Fig 55 Synchronization of two Mackey-Glass networks with different initial conditions using Method I with k = 1.1.

Fig 56 Average maximum Lyapunov exponent against k for the synchronization of two Mackey-Glass networks using Method II.

Fig 57 An attempt at synchronization of two Mackey-Glass networks with different initial conditions using Method II with k = 0.5.

The results of two Lorenz neural networks synchronized using Method I with k = 1.1 and using Method II with k = 0.3 can be seen in Fig 59 and Fig 61 respectively.

Fig 58 and Fig 60 show the graphs of maximum Lyapunov exponent of the difference of the signals against k of synchronization Method I and synchronization Method II respectively averaged over 10 sets of initial conditions.

The Delayed Chua Network has 10 inputs. The control was only applied to first input and the control constant used was k = 0.9 using Method I and k = 0.5 using Method II. The results of synchronization (the difference of signals of the two networks) can be seen in Fig 63 and Fig 65 respectively for Method I and Method II.

Fig 62 and Fig 64 show the graphs of maximum Lyapunov exponent of the difference of the signals against k of synchronization Method I and synchronization Method II respectively averaged over 10 sets of initial conditions.

5. Example: using the HŽnon neural networks to transmit a message

Finally we illustrate that how the synchronization of two iterative chaotic neural networks can be used to transmit a message. We sent a binary message as shown in Fig 66 using the HŽnon neural network defined above.

Fig 66 The binary message as 'blips' to be encoded into the HŽnon neural network transmitter.

Fig 67 The HŽnon network generated chaotic carrier containing a (masked) binary message.

Fig 68 Retrieved message on the error graph using synchronization Method I with k = 0.8.

A binary message was added to one of the input line of the network at regular intervals, a 'one' being a small spike and the absence of an encoded spike being taken to represent a 'zero', as shown in Fig 48. Here the encoded signal is retrieved by subtracting the synchronized output of network B from the received signal.

The signal sent from the transmitter appears to be chaotic as shown in Fig 67, the binary encoded signal being masked by the carrier. Using the synchronization Method I with k = 0.8 on the receiver end (on the HŽnon neural network), after the initial transient synchronization steps, the messages appear as several large blips on the error graph in Fig 68, i.e. a successful retrieval of the message from the chaotic carrier.

References

[Ashwin 1996] Ashwin, P, Buescu, J, & Stewart, I. (1996) Nonlinearity 9, 703--737.

[Fletcher 1987] Fletcher, R. (1987) Practical Methods of Optimization. (John Wiley & Sons), 2nd edition.

[Oliveira 1998] Oliveira, A.R.G. d & Jones, A.J. (1998) International Journal of Bifurcation and Chaos 8, 2225-2237.

[Parker1992] Parker, T & Chua, L. (1992) Practical Numerical Algorithms for Chaotic Systems. (Springer-Verlag, New York).

[Sano 1985] Sano, M & Sawada, Y. (1985) Physical Review Letters 55, 1082-1085.

Neural models of arbitrary chaotic systems: construction and the role of time delayed feedback in control and synchronization

[Supplementary materials and experimental results]

Antonia J. Jones, Alban P.M. Tsui and Ana G. Oliveira

CONTENTS

1 Probabilistic local stability

2 Examples of model construction

3. Delayed feedback control

4 Synchronization

5. Example: using the HŽnon neural networks to transmit a message

References