Finding the Optical Flow

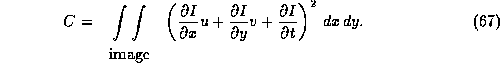
The above smoothness constraint is not necessarily entirely consistent with the optical flow constraint. We can express how much a solution for u and v deviates from the condition required by the optical flow constraint equation by evaluating

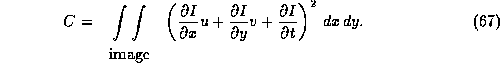
To meaningfully combine these two constraints, we use the technique of Lagrangian multipliers:

• Attempt to find a solution for u and v which minimises , where is a scalar.
  
• Typically we would make large if the intensity measurements were accurate, when we should expect C to naturally be quite small.
  
• On the other hand, if the original data were noisy, would be made quite small.
  
• Interactive adjustment will in general be required to find the best value for .

Minimising the resulting integral can be done by using standard techniques from the calculus of variations, which show that the functions u and v which are required satisfy the coupled pair of differential equations:

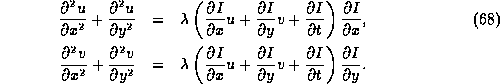
The derivatives of I for each pixel are obtained from the original image, and is chosen as above. An iterative method can then be used to solve these equations for u and v at each pixel.