2D Case

If f(x,y) is a function, for example the brightness in an image, its Fourier transform is given by

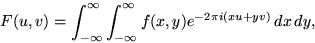$$F(u,v) = \int_{-\infty}^\infty\int_{-\infty}^\infty f(x,y) e^{-2\pi i (x u+y v)}\,dx\,dy,$$ (4)

and the inverse transform, as might be expected, is

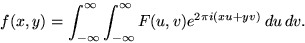$$f(x,y) = \int_{-\infty}^\infty\int_{-\infty}^\infty F(u,v) e^{2\pi i (x u+y v)}\,du\,dv.$$ (5)