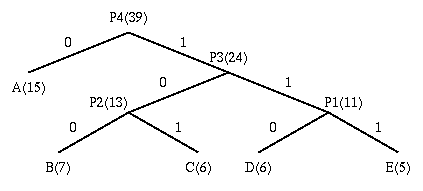
Huffman coding is based on the frequency of occurance of a data item (pixel in images). The principle is to use a lower number of bits to encode the data that occurs more frequently. Codes are stored in a Code Book which may be constructed for each image or a set of images. In all cases the code book plus encoded data must be transmitted to enable decoding.
The Huffman algorithm is now briefly summarised:
1. Initialization: Put all nodes in an OPEN list, keep it sorted at all times (e.g., ABCDE).
2. Repeat until the OPEN list has only one node left:
(a) From OPEN pick two nodes having the lowest frequencies/probabilities, create a parent node of them.
(b) Assign the sum of the children's frequencies/probabilities to the parent node and insert it into OPEN.
(c) Assign code 0, 1 to the two branches of the tree, and delete the children from OPEN.

Symbol Count log(1/p) Code Subtotal (# of bits)
------ ----- -------- --------- --------------------
A 15 1.38 0 15
B 7 2.48 100 21
C 6 2.70 101 18
D 6 2.70 110 18
E 5 2.96 111 15
TOTAL (# of bits): 87
The following points are worth noting about the above algorithm:
Number of bits needed for Huffman Coding is: 87 / 39 = 2.23