


Next: Belief Models and Certainty
Up: Basic Statistical methods --
Previous: Basic Statistical methods --
Bayesian statistics lie at the heart of most statistical reasoning systems.
How
is Bayes theorem exploited?
Herein lies a problem:
- All events must be mutually exclusive.
However in real world problems events are not generally unrelated. For example
in diagnosing measles, the symptoms of spots and a fever are related. This
means that computing the conditional probabilities gets complex.
In general if a prior evidence, p and some new observation, N then computing
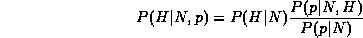
grows exponentially for large sets of p
- All events must be exhaustive. This means that in order to compute
all probabilities the set of possible events must be closed. Thus if new
information arises the set must be created afresh and all probabilities
recalculated.
Thus Simple Bayes rule-based systems are not suitable for uncertain
reasoning.
- Knowledge acquisition is very hard.
- Too many probabilities needed -- too large a storage space.
- Computation time is too large.
- Updating new information is difficult and time consuming.
- Exceptions like ``none of the above'' cannot be represented.
- Humans are not very good probability estimators.
However, Bayesian statistics still provide the core to reasoning in many
uncertain
reasoning systems with suitable enhancement to overcome the above problems.
We will look at three broad categories:
- Certainty factors,
- Dempster-Shafer models,
- Bayesian networks.



Next: Belief Models and Certainty
Up: Basic Statistical methods --
Previous: Basic Statistical methods --
dave@cs.cf.ac.uk
![]()
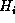 is true is equal to the ratio of the probability that E will be true
given
is true is equal to the ratio of the probability that E will be true
given 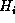 times the a priori evidence on the probability of
times the a priori evidence on the probability of 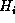 and the sum of the probability of E over the set of all hypotheses times the
probability of these hypotheses.
and the sum of the probability of E over the set of all hypotheses times the
probability of these hypotheses.