Version Spaces

Structural concept learning systems are not without their problems.

The biggest problem is that the teacher must guide the system through carefully chosen sequences of examples.

In Winston's program the order of the process is important since new links are added as and when now knowledge is gathered.

The concept of version spaces aims is insensitive to order of the example presented.

To do this instead of evolving a single concept description a set of possible descriptions are maintained. As new examples are presented the set evolves as a process of new instances and near misses.

We will assume that each slot in a version space description is made up of a set of predicates that do not negate other predicates in the set -- positive literals.

Indeed we can represent a description as a frame bases representation with several slots or indeed use a more general representation. For the sake of simplifying the discussion we will keep to simple representations.

If we keep to the above definition the Mitchell's candidate elimination algorithm is the best known algorithm.

Let us look at an example where we are presented with a number of playing cards and we need to learn if the card is odd and black.

We already know things like red, black, spade, club, even card, odd card etc.

So the is red card, an even card and a heart.

This illustrates on of the keys to the version space method specificity:

• Conjunctive concepts in the domain can be partially ordered by specificity.
• In this Cards example the concept black is less specific than odd black or spade.
• odd black and spade are incomparable since neither is more (or less) specific.
• Black is more specific than any card, any 8 or any odd card

The training set consist of a collection of cards and for each we are told whether or not it is in the target set -- odd black

The training set is dealt with incrementally and a list of most and least specific concepts consistent with training instances are maintained.

Let us see how can learn from a sample input set:

• Initially the most specific concept consistent with the data is the empty set. The least specific concept is the set of all cards.
• Let the be the first card in the sample set. We are told that this is odd black.
• So the most specific concept is alone the least is still all our cards.
• Next card : we need to modify our most specific concept to indicate the generalisation of the set something like ``odd and black cards''. Least remains unchanged.

• Next card : Now we can modify the least specific set to exclude the . As more exclusion are added we will generalise this to all black cards and all odd cards.
• NOTE that negative instances cause least specific concepts to become more specific and positive instances similarly affect the most specific.
• If the two sets become the same set then the result is guaranteed and the target concept is met.

The Candidate Elimination Algorithm

Let us now formally describe the algorithm.

Let G be the set of most general concepts. Let S be the set of most specific concepts.

Assume: We have a common representation language and we a given a set of negative and positive training examples.

Aim: A concept description that is consistent with all the positive and none of the negative examples.

Algorithm:

• Initialise G to contain one element -- the null description, all features are variables.
• Initialise S to contain one element the first positive example.

• Repeat
  • Input the next training example
  • If a positive example -- first remove from G any descriptions that do not cover the example. Then update S to contain the most specific set of descriptions in the version space that cover the example and the current element set of S. I.e. Generalise the elements of S as little as possible so that they cover the new training example.
  • If a negative example -- first remove from S any descriptions that cover the example. Then update G to contain the most general set of descriptions in the version space that do not cover the example. I.e. Specialise the elements of S as little as possible so that negative examples are no longer covered in G's elements.
  until S and G are both singleton sets.

• If S and G are identical output their value.
• S and G are different then training sets were inconsistent.

Let us now look at the problem of learning the concept of a flush in poker where all five cards are of the same suit.

Let the first example be positive:

Then we set

No the second example is negative:

We must specialise G (only to current set):

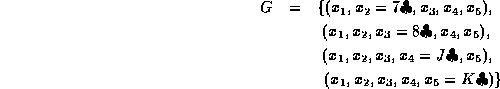
S is unaffected.

Our third example is positive:

Firstly remove inconsistencies from G and then generalise S:

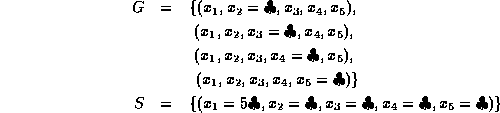
Our fourth example is also positive:

Once more remove inconsistencies from G and then generalise S:

• We can continue generalising and specialising
• We have taken a few big jumps in the flow of specialising/generalising in this example. Many more training steps usually required to reach this conclusion.
• It might be hard to spot trend of same suit etc.