


Next: Detecting Progress
Up: Planning System Components
Previous: Choice of best rule
- Previously rules could be applied without any difficulty as
complete systems were specified and rules enabled the system
to progress from one state to the next.
- Now we must be able to handle rules which only cover
parts of systems.
- A number of approaches to this task
have been used.
Green's Approach (1969)
Basically this states that we note the changes to a
state produced by the application of a rule.
Consider the problem of having two blocks A and B stacked on each
other (A on top).
Then we may have an initial state 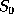 which could be described
as:
which could be described
as:
ON(
ONTABLE(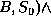
CLEAR(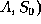
If we now wish to UNSTACK(A, B). We express the operation as follows:
[CLEAR(x,s) 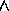 ON(x, y, s)]
ON(x, y, s)] 
[HOLDING(x, DO(UNSTACK(x,y),s)) 
CLEAR(y,DO(UNSTACK(x,y),s))]
where x,y are any blocks, s is any state and DO() specifies that an new
state results from the given action.
The result of applying this to state 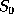 to give state
to give state 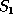 then we
get:
then we
get:
HOLDING(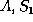 )
) 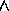 CLEAR(
CLEAR(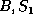 ).
).
There are a few problems with this approach:
- The frame problem
- -- In the above we know that B is still on
the table. This needs to be encoded into frame axioms that describe
components of the state not affected by the operator.
- The qualification problem
- -- If we resolve the frame problem the
resulting description may still be inadequate. Do we need to encode that
a block cannot be places on top of itself? If so should this attempt
fail?
If we allow failure things can get complex -- do we allow for a lot of
unlikely events?
- The ramification problem
- -- After unstacking block A,
previously, how do we know that A is no longer at its initial location?
Not only is it hard to specify exactly what does not happen (
frame problem) it is hard to specify exactly what does happen.
STRIPS (1971 ff.)
STIPS proposed another approach:
- Basically each operator has
three lists of predicates associated with it:
- a list of things that become TRUE called ADD.
- a list of things that become FALSE called DELETE.
- a set of prerequisites that must be true before the operator can be
applied.
- Anything not in these lists is assumed to be unaffected by the
operation.
- This method initial implementation of STRIPS -- has been
extended to include other forms of reasoning/planning (e.g.
Nonmonotonic methods, Goal Stack Planning and even Nonlinear planning --
see later)
Consider the following example in the Blocks World and the
fundamental operations:
- STACK
- -- requires the arm to be holding a block A and the other
block B to be clear.
Afterwards the block A is on block B and the arm is empty and these
are true -- ADD;
The arm is not holding a block and block B is not clear; predicates
that are false DELETE;
- UNSTACK
- -- requires that the block A is on block B; that the arm is
empty and that block A is clear.
Afterwards block B is clear and the arm is holding block A - ADD;
The arm is not empty and the block A is not on block B -- DELETE;
- See Exercises for more examples.
We have now greatly reduced the information that needs to be held.
If a new attribute is introduced we do not need to add new axioms for
existing operators. Unlike in Green's method we remove the state
indicator and use a database of predicates to indicate the current state
Thus if the last state was:
ONTABLE(B) 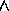 ON(A,B)
ON(A,B) 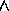 CLEAR(A)
CLEAR(A)
after the unstack operation the new state is
ONTABLE(B) 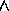 CLEAR(B)
CLEAR(B) 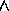 HOLDING(A)
HOLDING(A) 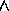 CLEAR(A)
CLEAR(A)



Next: Detecting Progress
Up: Planning System Components
Previous: Choice of best rule
dave@cs.cf.ac.uk
![]() which could be described
as:
which could be described
as:

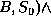
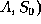
ON(x, y, s)]
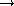
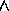
![]() to give state
to give state ![]() then we
get:
then we
get:
![]() )
) ![]() CLEAR(
CLEAR(![]() ).
).
![]() ON(A,B)
ON(A,B) ![]() CLEAR(A)
CLEAR(A)
![]() CLEAR(B)
CLEAR(B) ![]() HOLDING(A)
HOLDING(A) ![]() CLEAR(A)
CLEAR(A)