Cutting, Packing and VLSI Layout

Christine L Mumford and Pearl Y Wang

1  Overview of Research

We have dealt principally with algorithms for two dimensional cutting and packing, in which smaller rectangles are cut from or packed into larger rectangular shapes. We have focussed our research on slicing floorplans and guillotine cutting approaches (See Figure 1). Such patterns are produced by applying repeated edge-to-edge cuts. These methods are fast and work with considerably reduced search spaces, and we have obtained some excellent results using these approaches. In many senses, cutting problems can be equally modelled as packing problems, and vice versa. Both involve optimizing layout to minimize waste, known as dead space (packing) or trim waste (cutting). Two dimensional cutting problems are often referred to as cutting stock problems, and two dimensional packing problems are frequently called 2D bin packing problems if packing into rectangular shapes of fixed height and width dimensions, or strip packing problems, if packing into a rectangle of fixed width and (effectively) infinite height. Cutting paper or cloth from very large stock rolls provide typical applications of strip packing.
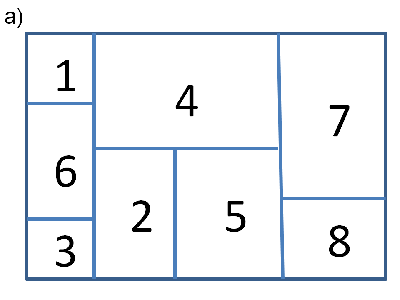
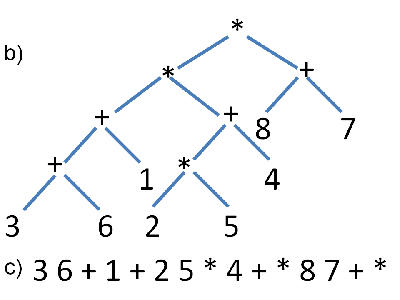
Figure 1: An example of a guillotine cutting pattern or slicing floorplan (a), a corresponding normalized slicing tree (b) and normalized postfix expression (c)
rectanglecut.png
slicingtree.png
Our main contributions to research are:
Figure 2: Data instance nice500, rectangles cut with "nice" dimensions
nice500.png
Figure 3: Data instance path500, rectangles cut with "pathological" dimensions
path500.png
In addition, all our data sets available form here, and some past MSc students have produced some excellent information pages and applet demonstrations on some basic guillotine cutting/packing heuristic algorithms:
Level and Shelf Algorithms, by Heidi Smith
Slicing Floorplans by Lisa Daniels

2  Introduction

Various industrial problem require a set of rectangles of specific sizes to be cut out of larger stock rectangles to satisfy customer demand, for example in glass, wood or paper cutting. Depending on the limitations or nature of the material, it is may necessary or convenient to use machinery that can perform only guillotine cuts, which are top to bottom or side to side cuts.
In the next two sections we will review some very simple heuristic algorithms for cutting/packing. We have implemented these and used the results to compare with those obtained by our genetic algorithm in some of our papers. More details, algorithms and demonstrations can be found on level and shelf algorithms here. Following this, we briefly discuss slicing floorplans and postfix expressions, which provide the basis for most of our cutting and packing research. More information and a demonstration on slicing trees and postfix expressions can be found here.

2.1  The Level Oriented Algorithms

The level oriented algorithms were first introduced in [9]. To implement a level oriented algorithm, the items are first pre-sequenced by non-increasing height, and then the packing is constructed as a series of levels, each rectangle being placed so that its bottom rests on one of these levels. The first level is simply the bottom of the bin. Each subsequent level is defined by a horizontal line drawn through the top of the tallest rectangle on the previous level. It is easy to see how edge-to-edge cuts can reproduce these packing patterns. Each shelf is cut using a horizontal cut, then the rectangles sitting on the individual shelves are divided by making vertical cuts, finally trimming off the surplus from to tops of the rectangles using horizontal cuts.
Figure 4:
NF-FFDH.png
In the Next Fit Decreasing Height (NFDH) algorithm, rectangles are packed left justified on a level until the next rectangle will not fit, in which case it is used to start a new level above the previous one, on which packing proceeds. The run time complexity of NFDH (excluding the sort) is linear, just placing one rectangle after another in sequence. The First Fit Decreasing Height (FFDH) algorithm places each rectangle left justified on the first (i.e. lowest) level in which it will fit. If none of the current levels has room, then a new level is started.
The FFDH heuristic can be easily modified into a Best Fit Decreasing Height (BFDH) and a Worst Fit Decreasing Height (WFDH) heuristic. BFDH packs each piece onto the best level (i.e. the one with least remaining horizontal space) on which it will fit. WFDH packs the piece into the largest remaining horizontal space where it will fit. These four approaches are two-dimensional analogues of classical one-dimensional packing heuristics. The run time complexity for FFDH, BFDH and WFDH is O(n lgn) where n is the number of rectangles being packed. Figure 4 illustrates the NFDH and FFDH packings for the same six rectangles.

2.2  The Shelf Algorithms

The on-line packing heuristics proposed by [8] can be used when pre-ordering of the input data is to be avoided. For example, if the rectangles arrive to be packed at different times, so it is not possible to pre-sort them. The shelf algorithms are modifications of the Next-Fit and First-Fit approaches. Rectangles whose dimensions are between 0 and 1 are packed on shelves whose heights are set by a parameter r where 0 < r < 1. Shelf sizes have the form rk and each rectangle of height h, rk+1 ≤ h ≤ rk is packed into a shelf having height rk. Thus, the motivation for the use of r is to limit the amount of vertical wasted space which is allowed on each shelf.
Using the Next-Fit approach, the Next-Fit Shelf (NFS r) algorithm packs each piece as far to the left as possible on the highest shelf with height rk where the rectangle height h, rk+1 ≤ h ≤ rk. If there is no room on this shelf, a new one is created having height rk. In the First-Fit Shelf (FFS r) algorithm, the lowest shelf of the correct height on which the rectangles will fit is chosen. Examples of NFS r and FFS r packing are shown in Figure 5.
Figure 5:
Shelf.png

2.3  Slicing Floorplans and Reverse Polish (Postfix) Notation

We now move to generic guillotine patterns/slicing floorplans. A slicing floorplan is a rectangular pattern with n basic rectangles that can be obtained by recursively cutting a rectangle into smaller rectangles using a series of vertical and horizontal edge-to-edge (i.e., guillotine) cuts (see Figure 1 a)). A slicing floorplan can be represented in the form of a binary tree, called a slicing tree (Figure 1 b)), in which each internal node of the tree is labelled either * or +, corresponding to a vertical or a horizontal cut respectively. Each leaf represents a basic rectangle and is labelled between 1 and n, where n is the total number of basic rectangles. A slicing tree can be represented, alternatively, using a postfix expression (Figure 1 c))). The postfix expression is derived by carrying out a post-order traversal, and corresponds more readily to a packing viewpoint rather than cutting. Figure 1 b) represents a skewed slicing tree which is a representation that provides a unique depiction of a given slicing floorplan [11]. Figure 1 c) represents a normalized postfix expression, which provides a linear representation for a skewed slicing tree. A normalized postfix expression is easily recognized because adjacent operators alternate between `+' and `*'.
Figure 6: Binary operations combining rectangles in pairs to produce a slicing floorplan
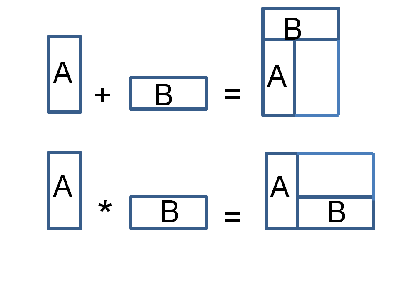AandB.png
Figure 6 shows the two binary operations, `+' and `*', used to combine rectangles (and rectangle combinations) in pairs to produce an alternative packing view of a slicing floorplan. `+' puts B on top of A, and `*' puts B on the right of A. In the example depicted in Figure 6, the two rectangles A and B combine under + and * to form L-shaped modules. During the cutting or packing process, however, each L-shaped module (and any other shaped modules which are not rectangular) will be replaced by the smallest possible enclosing rectangle, resulting in the creation of dead space (or trim waste) in the floorplan.

3  Downloadable Documents

Our papers deal with guillotine cutting/slicing floorplans involving TWO types of rectangles:
  1. rigid (or hard) rectangles with fixed height and width dimensions, and
  2. flexible (or soft) rectangles with fixed area but varying height/width within set boundaries for maximum and minimum aspect ratios (i.e., height:width fraction).
Hard rectangles are packed in [6] and [2]. Both papers deal with strip packing and explore some small and large problem instances, comparing the performance of our GA with simple construction heuristics. We also try data sets with different characteristics: "nice" data with sizes and shape dimensions (Figure 2) that are not extreme, and "path" data with very variable shaped rectangles with many that are long and thin (Figure 3). The data generation method is described in [7].
Soft rectangles for VLSI physical layout are dealt with in [3] and [4], and for facility layout in [5].

Data

Strip packing data generated by the software described in [7] can be downloaded as follows: The format of this data is as a list of "height width" dimensions of n rectangles.
VLSI data adapted from the MCNC (https://www.mcnc.org/) benchmarks , ami33, ami49 and playout, plus an extra instance, f100, generated by ourselves, and be downloaded here. These data files are used in [3] and [4].
The format of this data is a list of the areas of the n rectangles. In the papers we carry out shape optimization of the individual rectangles simultaneously with the optimization of the enclosing rectangle, subject to user-provided aspect ratio limitations.
Data for the facility layout problem used in [5] was obtained courtesy of the authors of [10] and can be downloaded from here.
Please cite our papers if you use our data.

References

       This Research

[1]
Dorband, John E., Mumford, Christine L. and Wang, Pearl Y., Developing an aCe Solution for Two-Dimensional Strip Packing. In 18th International Parallel and Distributed Processing Symposium, Volume 16, pages 261b, IEEE Computer Society, Los Alamitos, CA, USA, 2004.
[2]
Mumford-Valenzuela, Christine L., Vick, Janis and Wang, Pearl Y., Heuristics for large strip packing problems with guillotine patterns: An empirical study. Chapter 24 of Metaheuristics: Computer Decision-Making. Edited by D. Z. Du and P. M. Pardalos, Series Editors, pages 501-522, Kluwer Academic Press, 2003.
[3]
Valenzuela, C. L. and Wang, P. Y. A Genetic Algorithm for VLSI Floorplanning. In Parallel Problem Solving from Nature - PPSN VI, Lecture Notes in Computer Science 1917, pages 671-680, Springer, 2000.
[4]
Valenzuela, C. L. and Wang, P. Y. VLSI Placement and Area Optimization Using a Genetic Algorithm to Breed Normalized Postfix Expressions. IEEE Transactions on Evolutionary Computation, Vol. 6, No. 4, pages 390-401, August 2002.
[5]
Valenzuela, C. L. and Wang, P. Y. Breeding Normalized Postfix Expressions for the Facility Layout Problem. Metaheuristic International Conference 2001 (MIC'2001), Porto, Portugal.
[6]
Valenzuela, C. L., Wang, P. Y. Heuristics for Large Strip Packing Problems with Guillotine Patterns: an Empirical Study. Metaheuristic International Conference 2001 (MIC'2001), Porto, Portugal.
[7]
Wang, P. Y and Valenzuela, C. L. Data Set Generation for Rectangular Placement Problems. European Journal of Operational Research, Vol 134(2):150-163, 2001.

References

[8]
Baker, B.S. and Schwarz J.S. Shelf Algorithms for Two-Dimensional Packing Problems. SIAM Journal of Computing, 12:508-525, 1983.
[9]
Coffman Jr., E. G., Garey, M. R. and Johnson, D. S. Performance Bounds for Level-Oriented Two-Dimensional Packing Algorithms. SIAM Journal of Computing, Vol 9:808-826, 1980.
[10]
Kado, Kazuhiro, Ross, Peter and Corne, David. A Study of Genetic Algorithm Hybrids for Facility Layout Problems. Proceedings of the 6th International Conference on Genetic Algorithms. 498-505, Morgan Kaufmann, 1995.
[11]
Wong, D. F. and Leong, H. W. and Liu, C. L. Simulated Annealing for VLSI Design, Kluwer Academic Press, Boston MA, 1988.


File translated from TEX by TTH, version 3.87.
On 27 Feb 2011, 16:59.